- 例題3
- 底面積が400㎠の容器Aと底面積が500㎠の容器Bがあります。Aに、ある量の水を入れました。その後、Aから半分の量の水をBに移したところ、AとBの水位の差は、2.5cmでした。はじめにAに入れた水量は何Lですか。
- 解説
-

ん?
突然難しくなりましたね・・・
逆比の構造が、文章題の中でどのように表れるか慣れていこうね。
ここからが逆比の本番だと言えます!わからないときは整理するしかないよ。
図にかけるかな?
とにかくやってみます。
Aから半分の量の水をBに移す・・・
AとBの水位の差は、2.5cm
AとBのどちらが水位が高いのか・・・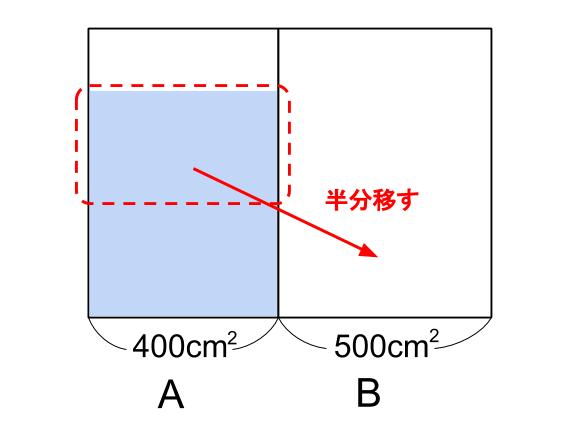

そうだね!
そのあたりのことを考えないといけない問題だってことがわかったね。
AにもBにも同じ量の水を入れるのだから、底面が広いBの方が水位が低くなりますね。
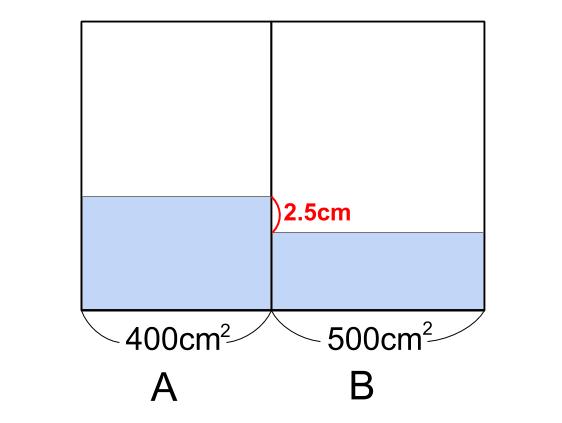

うまくいってるね。
つまり、この問題は何に着目すべきなのか。
もうわかったでしょ?
「底面積」と「水位」と「水量」ですね。
この3つは
「底面積」×「水位(高さ)」=「水量(体積)」
という関係がありますね。
その通り!
問題で書かれていることを式にしてみようね。
はじめにAに入れた水量を半分にしているから、2:1だ。
はじめの水量を②、移したあとの水量は①とします。「底面積」×「水位(高さ)」=「水量(体積)」
A:400×?=①
B:500×?=①なるほど!
水量が①で「同じ」なんだ!つまり、400×?=500×?(=①)
これは逆比の形ですね!
素晴らしい。
正解まであとわずかですよ!
400×?=500×?(=①)
だから、水位(高さ)は逆比で、5:4
400×5=500×4(=①)
水位の差が2.5cmなのだから、
5と4の差、1=2.5cmだから、
5=12.5cm
4=10cm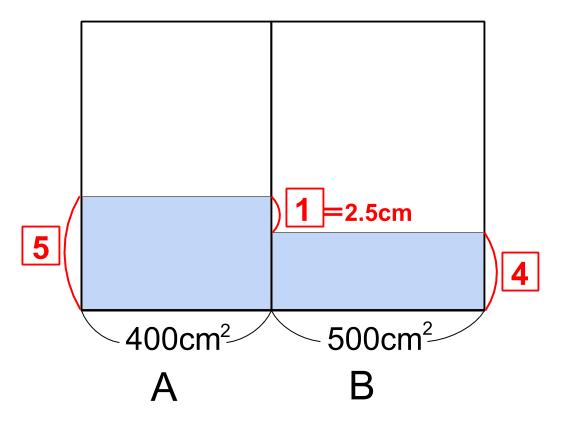

よって、水量は、
400×12.5 =500×10=5000(㎤)=5(L)つまり、はじめにAに入れた水量は、
5×2=10
10Lです!
大正解!おめでとう。
今回の問題のように、2つの容器に水を入れる問題で逆比を使うのは大定番パターンなのです。
A:400×?=①
B:500×?=①と整理した後に、
改めて、400×?=500×?(=①)
と書き直すのも良いのだけれど、A:400×5=①
B:500×4=①と逆比の情報をすぐに入れてしまってもOKだし、その方が簡略化して解けておススメかな。細かい話なのでどちらでもいいけどね。
