異なる2種類の比の処理
異なる2種類の比の処理の練習
例題
はじめのお金の \(\displaystyle \frac{1}{4}\) より150円安い商品Aを買いました。残りのお金の \(\displaystyle \frac{2}{5}\) で商品Bを買ったところ、残りのお金は商品Aの値段の2倍でした。はじめいくら持っていましたか。
解説

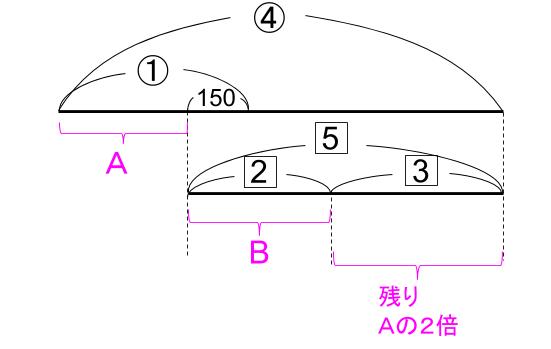
線分図で整理しますね。

Aは、①ー150
だから、Aの2倍は、
(①ー150)×2=②ー300
これが3と等しい。
②ー300=3
あともう1つ等式が必要ですね。
Aを買った残りは、③+150=5
これで消去算で解けます!

その通り。
素晴らしいですね。
あとは、計算処理だけで答えが求まりますね。
(ア)②-300=3
(イ)③+150=5
(ア)を3倍、(イ)を2倍すると、
(ア×3)⑥-900=9
(イ×2)⑥+300=10
差をとると、1=1200
より、①=1950
はじめは④なので、④=7800
7800円と求まります。

ちょっと別解も見ておこうか。
まあ、参考程度になんですけどね。
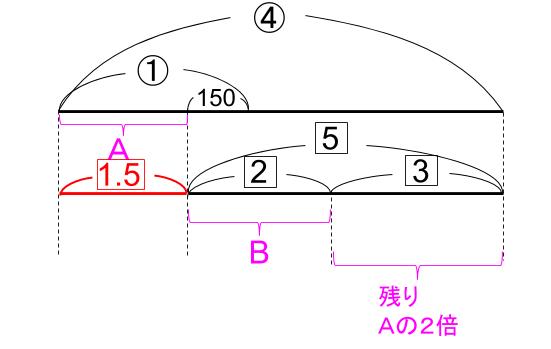
残りがAの2倍というところだ。
残りが3ならば、Aが1.5だということだ。

1.5+150=①
って等式がつくれますね。

まあ間違ってないけどね。
もう消去算はいらないじゃないですか。
〇と□が共通部分でそろえられるでしょ。

はじめの金額だ!
④=6.5
ですね。
で、えっと・・・いくつにそろえたらいいんだ?

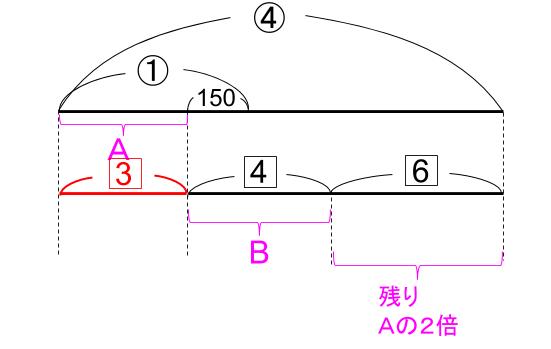
□のほうが小数であつかいづらい。
だから、2倍すればい。
1.5:2:3=3:4:6
だからね。

④=13
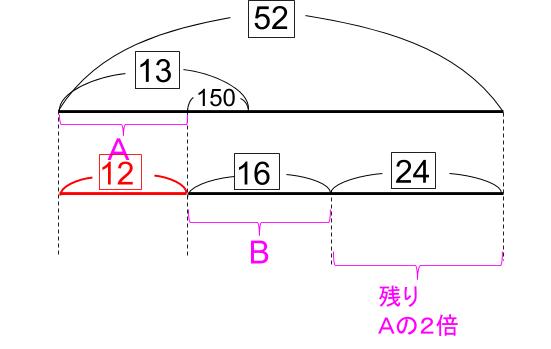
4と13の最小公倍数52を使う。
改めて、全体を52とします。
52の \(\displaystyle \frac{1}{4}\) は13
52を3:4:6にわければ、12と16と24

1=150だから、はじめのお金は52=150×52=7800
求まりました。7800円です。

正解です。
今見てきた別解は、「気づき」が必要だよね。
このような「気づき」がなくても、計算処理だけでゴリ押しできてしまうのが消去算の強さなのです。
消去算がいかに便利で大事なものか知っておきましょう。