食塩水の総量に着目する
同時に等量交換・同じ濃さ
例題1
容器Aには5%の食塩水が200g、容器Bには13%の食塩水が600g入っています。それぞれの容器から同じ量の食塩水をくみ出しました。Aからくみ出した食塩水をBに、Bからくみだした食塩水をAに入れてよくかきまぜると、2つの容器の食塩水の濃度が同じになりました。
(1) この操作の後、食塩水の濃度は何%になりましたか。
(2) それぞれの容器からくみ出す食塩水は何gですか。
解説

これは今までの複数回混合と違いますよね。

うん。そうだね。
今までは、Aからくみ出した食塩水をBにいれてよく混ぜて、
それからBの食塩水をくみ出してAに戻していた。
順番に、2段階で混合をしていたんだよね。
今回はA、Bからそれぞれ同時にくみ出して、
AからのくみだしをBへ
BからのくみだしをAへ混ぜている。
同時に、2つの混合をしているんだね。

くみだした量も、濃さもわからない。わからないことだらけですね・・・
どこから解いたらいいのかまったくわかりません。

これははじめて解くタイプだからね。
わからなくても仕方がない。ポイントを教えるよ。
いっしょに解いていこう!

Xgずつくみ出して交換して、どちらもア%になったとします。
これは面積図で以下のようにまとめられる。
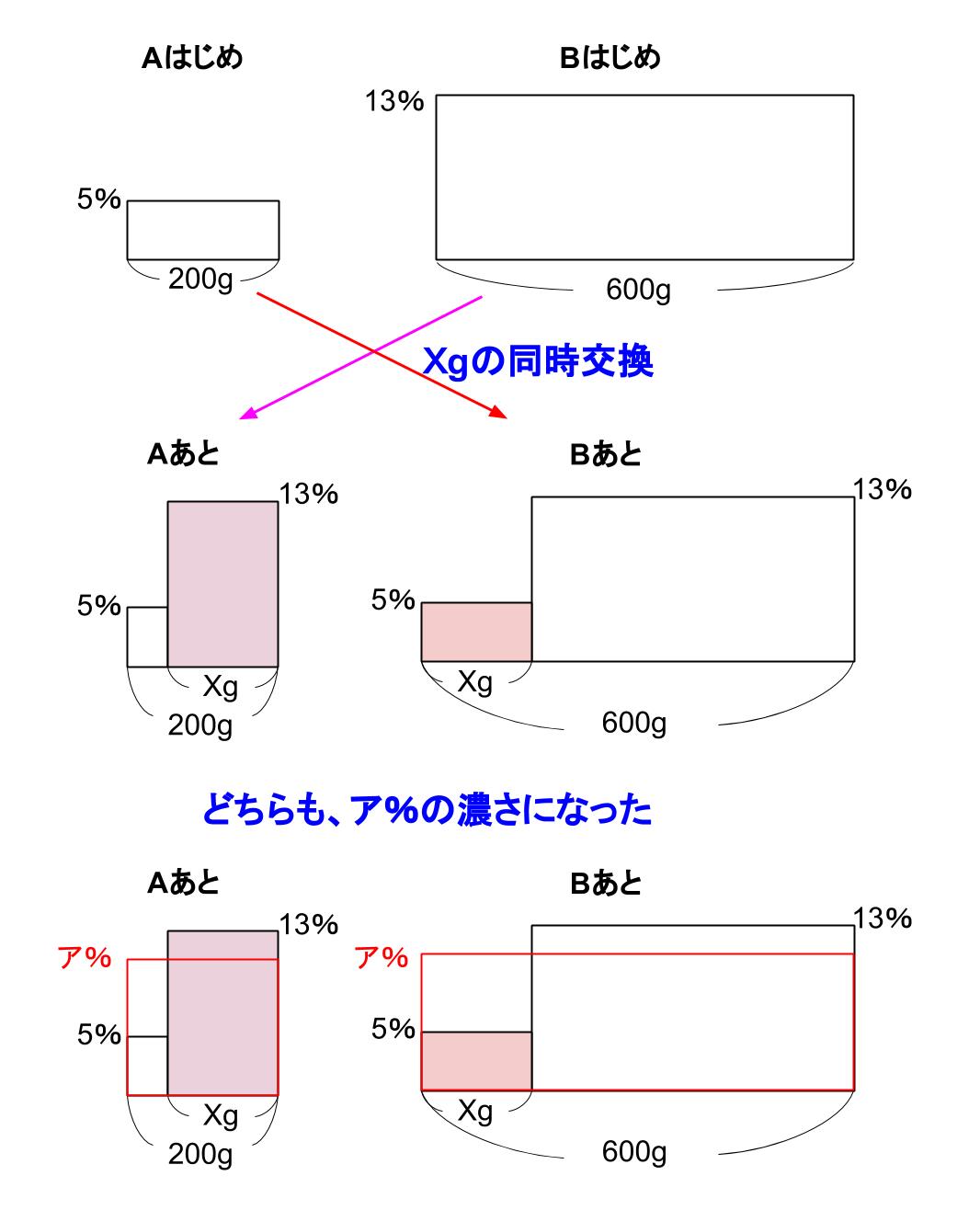

ちなみにこの図は、学くんが自分で解くときにはかかなくて良い図です。問題の意味や仕組みを、しっかりと理解してもらうための図だからね。
問題を解くときに、毎回この図をかくのではさすがにたいへんすぎるからね。

さて、解いていくよ。
「はじめの交換する前の食塩水どうしをすべて混ぜた食塩水」
と
「交換の後にできた2つの食塩水を混ぜた食塩水」
はまったく同じものになります。
わかるかな?

確かにそうですね。
「総量」は一定ですからね。
何かが増えたり減ったりしてないです。

そういうことです。
そして、この2つの食塩水の濃さについて見てみるんだ。
「はじめの交換する前の食塩水どうしをすべて混ぜた食塩水」の濃さは、
A:5%を200gと B:13%を600gを混ぜた食塩水の濃さであり、これは簡単に計算できるね。
濃さは11%です。
何の工夫もなくただ普通に計算で求めるだけだよね。面積図で求めてもよいです。
で、次。
「交換の後にできた2つの食塩水を混ぜた食塩水」の濃さは、
2つのア%の濃さの食塩水をまぜるのだから、まぜたあとの濃さもア%になります。
つまり、ア=11なのです。
これで(1)が求まったわけだ。
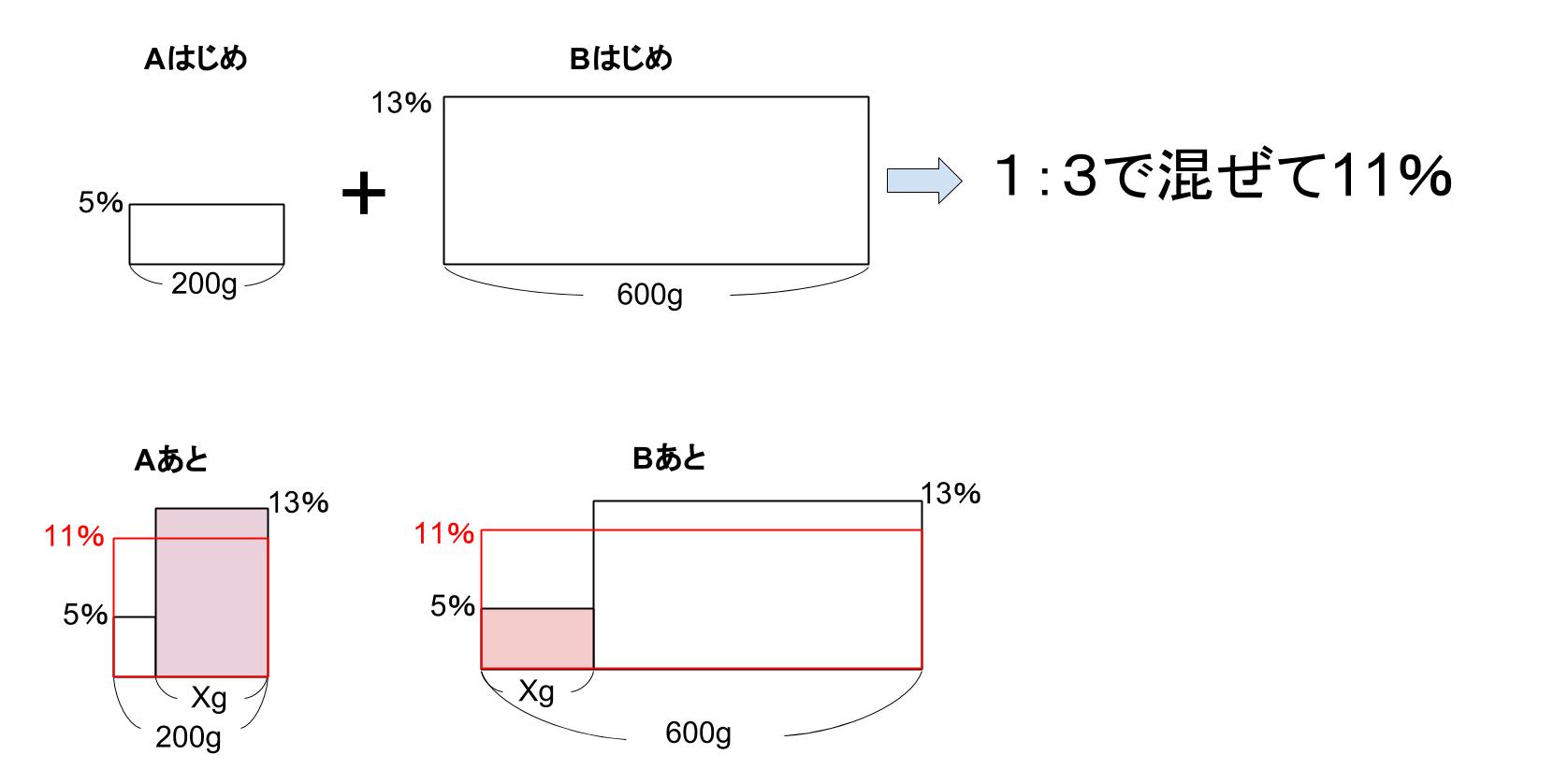

交換後は、AもBも濃さが11%になっていて、
それらを混ぜればもちろん濃さが11%になる・・・
なるほど、全部混ぜた濃さが、交換前も交換後も同じ・・・うまい解き方ですね。

これは有名問題なんですよ。
とにかくこの解法を覚えてしまいましょうね。
で、次は交換した量、Xgを求めたいわけだ。

5%と13%を混ぜて11%になったということですから、面積図で簡単に求まります!
Aで解いてもBで解いても、X=150 と求まります!
150gの交換をしたということです。
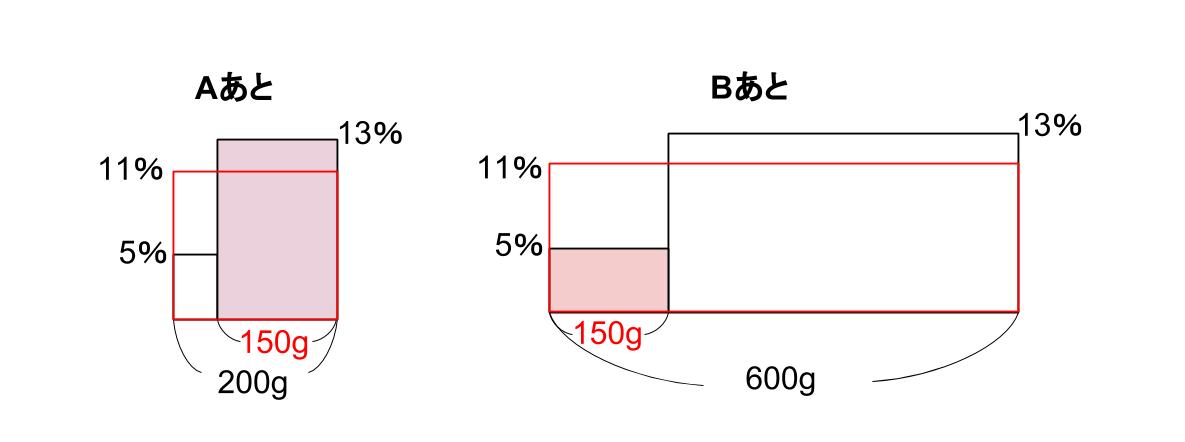

大正解!
なんだけれど、もっと本質的な解法も理解しておいて欲しい。
AもBも、どちらも、5%と13%をまぜて、11%にしているのだから、5%と13%を同じ比率で混ぜていることがわかります。
そして、その比率を、先ほど学くんは面積図を使って計算をしたのです。
1:3でしたね。
しかし、この比率は計算をしなくてもすぐにわかることなんだ。
なぜなら、はじめの食塩水を2つ混ぜたら11%になるのだから、
「5%」と「13%」は1:3の比率でまぜると11%になるのです。
※「5%200g」と「13%600g」をまぜると11%になる。
だから、AもBも、「5%」と「13%」を1:3の比率でまぜたということがわかります。
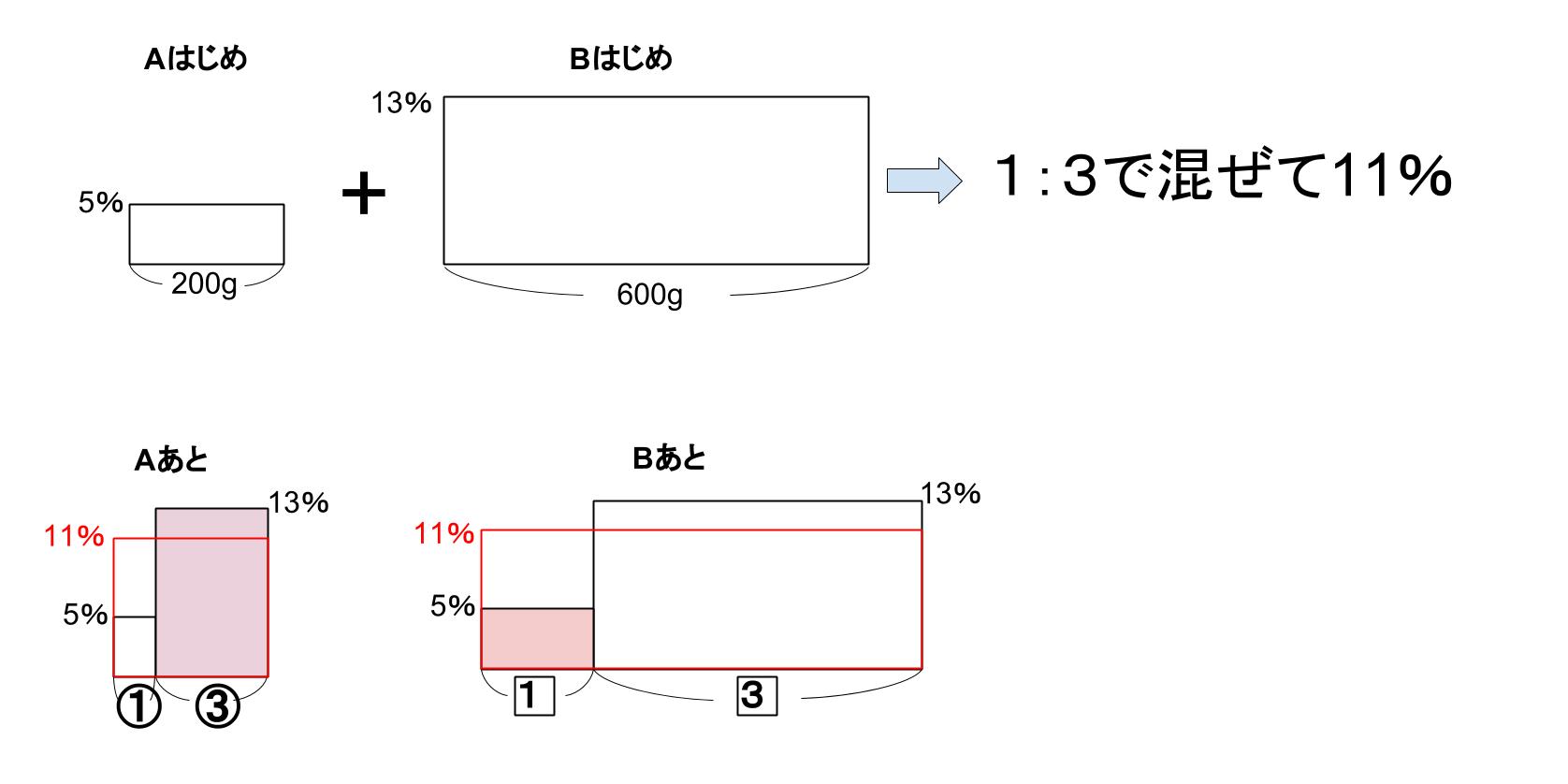

なるほど!
Aにできた濃さ11%の食塩水200gは、5%と13%を、1:3の比率で混ぜてできているのだから、200gを1:3に比例配分して50gと150g
150gがBからやってきた食塩水。つまり、150gの交換をしたと求まる!
うまい解き方ですね。

Bの方でも確かめれば
Bは600gを1:3に比例配分して150gと450g
150gがAからやってきた食塩水で、同じ答えを得る。
この150gを求めるためには、(1)の結論11%は一切使っていないことを確認しておこう。
(1)とは無関係に(2)を求めることができるんだ。
全部まぜると何%になるのか、計算で求めなくとも、1:3の比率で混ぜたことはわかるからね。

確かに。
はじめの5%と13%が1:3だったから・・・しか使ってないですね。

同時に等量交換をして、同じ濃さになる。
とても特徴のある問題だね。
しっかりと解法を理解・暗記しておこうね。
別解

「全部まぜたものが、はじめとあとで同じ」
という視点で解いたのだけど、「食塩の量」に着目してみても解けます。
やってみてごらん。

食塩の量に注目ですね。
Aはじめ:5%の食塩水が200gだから、食塩は10g
Bはじめ:13%の食塩水が600gだから、食塩は78g
交換のあとは・・・
濃さは分からない・・・どちらも濃さがア%になったとする。
全体量は、同じ量の交換だから、はじめと同じになる。
A後:ア%の食塩水が200g
B後:ア%の食塩水が600g

AとBは同じ濃さになったのだから・・・
同じ濃さの食塩水がAには200g、Bには600gあるんだよ。
とけている食塩の量も、200:600=1:3にわかれているんだ。
合計88gの食塩は、22gと66gにわかれている。

なるほどー。
A後:ア%の食塩水が200gに食塩は22g
B後:ア%の食塩水が600gに食塩は66g
A、Bどちらで計算しても、濃さは11%!
うまくいっています。答えが見つかりました。
さっきと同じ答えが出ましたね。

お見事です。正解。
「食塩の量の総量は、はじめとあとで同じ」という解き方でした。
