1:食塩水の導入
1:食塩水の導入

あれ、先生。授業なのにジュース飲んでっ!!

あー、おいしかった。ところで
オレンジジュースに果汁100%とか果汁50%って表示があるのは知ってる?

知ってます(ぼくも飲みたかった!)

意味は分かるかな?

100%は全部って意味だから、
多分果汁100%は、全部オレンジの果汁です。

おっ!ご名答。正解だよ。
先生の飲んでいるオレンジジュースは、果汁50%だ。
オレンジ果汁が半分(50%)と、残り半分(50%)は別の何かを混ぜてつくたものだ。

別の何かって?

うん、ジュースのメーカーに聞かないとわからないけど、何か人工的な液体だよ多分。

砂糖水かな?

それはわからないけどね。
さて、今日の本題は食塩水。
食塩水は割合の問題の代表選手なんだよ。

食塩水って理科みたいです。

理科で食塩水について学習したことがあるのかな?
食塩水はどうやってつくる?

水に食塩を入れてとかします。

うん。そうだよね。
他には何も入っていない。
食塩水は、食塩と水だけでできている。
まずはこの基本事項を押さえておこうね。
さて、下の2種類の食塩水について考えてみよう。
導入例題1
Aは水42gに食塩8gをとかした食塩水。
Bは水120gに食塩30gをとかした食塩水。
AとBのどちらの方がしょっぱい食塩水ですか。


どう?実際に味見をしないで、どうやったらわかるだろう?

Bの方が食塩が多いです。だから多分その逆をついてAの方がしょっぱい。
先生はきっとそんな問題を出す人です。

・・・あのさ・・・
そういう勘ぐりもね、頭の使い方としては悪くないんだけどね。
今はまず算数の力を伸ばしていこうぜ。

そうですね。
Aが3倍あれば、Bと同じ量になりますね。


とけている食塩は「A×3」は24gで「B」は30g、
Bの方が多いので、Bの方がしょっぱいです!

素晴らしい。
正解だよ。
食塩の量だけでは単純に比べられないよね。
しょっぱいということは、それだけ食塩の「割合」が大きいということだよね。

食塩を1kgとかした食塩水だって、プールにとかしたのならば、あまりしょっぱくない食塩水になりますね。

そういうことです。
ところで、これは割合の単元で似たような問題をやったんだけど覚えているかな?
「吹奏楽部と演劇部、どちらが女子だらけの部活なのか」という問題。
今回は
「どちらが食塩だらけの液体(食塩水)なのか」という問題なんだ。
そっくりでしょ。
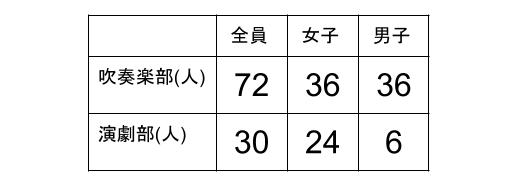

「全体の何倍が女子なのか」という割合で、女子だらけかどうかを判定しました。
吹奏楽部は、全体の \(50%\) が女子
演劇部は、全体の \(80%\) が女子
ですね。
ということは、食塩水では、
「食塩水全体の何倍が食塩なのか」という割合に着目するんですね。

その通り!!
この
「食塩水全体の何倍が食塩なのか」
という割合のことを、
「食塩水の濃さ」
というんだ。
食塩水の濃さ、は百分率(%)で表します。
食塩水Aを例に説明するね。


まず「濃さの定義」から明らかに、
(全体の量)×(濃さ)=(食塩の量)
という式が成り立ちます。
そしてこの式から明らかに、
(濃さ)=\(\displaystyle \frac{食塩の量}{全体の量}\)
です。
「濃さ」はさっきも言った通りだけど、百分率(%)で表します。
食塩水Aを例にすると、
\(\displaystyle \frac{8}{50}\)×100=16(%)です。

「食塩水全体の16%が食塩」ということですね。
50×0.16=8
食塩が8g
なるほど。

これらはいわゆる公式です。
これはきっちりと暗記しなくてはならないよ。
「食塩水の濃さ」という言葉の意味そのものだから、考えて導くものじゃない。
しっかりと暗記です。
では食塩水Bの濃さも出してみよう。
Bの方がAよりもしょっぱいことを数値で確認するよ。

Bは全体が150gで、食塩が30gだから、濃さは、
\(\displaystyle \frac{30}{150}\)×100=20(%)です。


Aは16%
Bは20%
食塩の割合は、Bの方が大きい。
つまり、Bの方が食塩だらけの食塩水です。
つまり、Bの方がしょっぱいことが分かります。
ところで、この「食塩水の濃さ」は「オレンジジュースの果汁」とそっくりだってわかるかな?

全体の半分が果汁なら、果汁50%。
全体の何倍が果汁なのか。
全体の何倍が食塩なのか。
確かに同じですね。

そう。もし食塩水の濃さが、何のことだかわからなくなったら、オレンジジュースと果汁のことを思い出すと良いですね。
