例題7
1個100円の商品を480個仕入れ、仕入れ値の6割増しの定価で売りはじめました。売れ残ったので、残りは定価の4割引きで売ったところ全部売り切れ、全体では2割4分の利益がありました。定価で売れた個数を求めなさい。
解説

「全体では2割4分の利益」
これがはじめて見る言葉ですね。

そうだね。
「商売全体で2割4分の利益」という意味だよ。
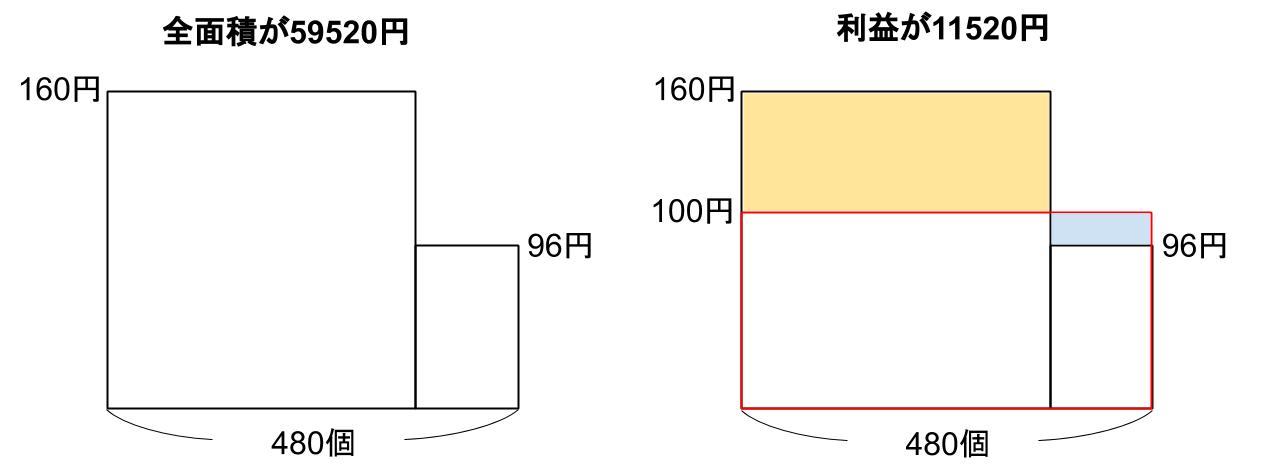
160円で1個売ると60円の利益、
96円で1個売ると4円の損、
これらを全部集めると「2割4分の利益」という意味だ。

「仕入れ値全体の2割4分の利益」ということですね?

はい、そういうことです。
仕入れ値全体は、100✕480(円)
これの2割4分が利益だから、利益は、
100✕480✕0.24(円)

利益は、
100✕480✕0.24=11520(円)
で、これって前にもやったつるかめ算ですよね。
利益だけに着目なら弁償するやつ。

その通りです。
あとはゴリゴリ計算していけば答えは出ます。
でもね、この後の計算は少しだけ面倒ですね。
計算が面倒になるような数値設定になっています。

そうかも・・・480✕160も480✕96もちょっと面倒ですね。

実は、別解を紹介するためにこの問題を扱っています。
計算がスッキリ楽な別解です。
ズバリ、「平均」なのです。

ほお・・・

「商売全体で2割4分の利益」という言葉の意味を考えてみましょう。
これって、「すべての商品を2割4分増しの定価」で売ったのと同じことです。

えっと・・・
確かにそんな気がします。するかな・・・

くわしく見ておきましょうか。
「全体の売上金額」は全仕入れ値の1.24倍だから、
「全体の売上金額」=100✕480✕1.24
この計算をする必要はないですからね、面倒です。
このかけ算の順序を変えましょう。
「全体の売上金額」=100✕1.24✕480
これってつまり、
「全体の売上金額」=124✕480
124円の商品を480個売ったときの売上金額と一致します。

なるほど・・・
では面積図にしますね。
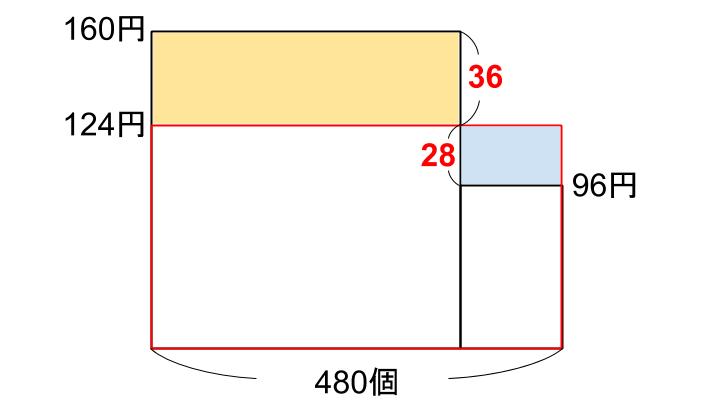

たての比が、36:28=9:7
だから、横の比が7:9
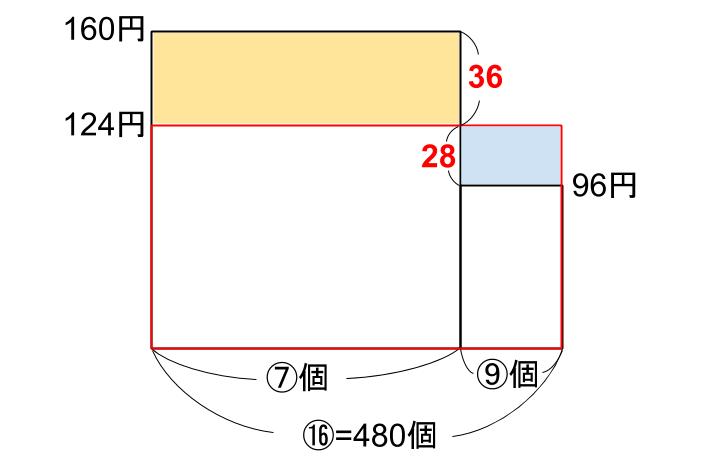

⑯=480なので、
⑦=210
なるほど!
すごい計算スッキリです。
楽ですね!

大正解です!
面積図を使うことで、「つるかめ算」や「平均」との関連性も理解しやすいと思います。
商品を複数扱う問題は面積図です!
