3:文章題へ

さて、今まで見てきた状況だけど、文章題として下の例題のように出題されるよ。
例題1
八百屋さんが、メロンに原価の6割増しの定価をつけました。メロン1個の定価が800円のとき、このメロンを1個売ることでえられる利益はいくらですか。
解説

文章だけ読んでもピンとこないですね。なんだか難しそうです。
やっぱり普段使わない言葉ばっかりだし。

そうだね。
それはまだ、言葉の意味をきちんと覚えていなかったり、商売の全体像が明確につかめていないからなんだ。
だから、必ず先生がまとめたような図(式)をかくこと!
めんどうがらないでかくことで、正確な理解が得られるからね。
この例題なら下のようになるよ。どこがわかっていて、どこがわからないのか。
全体像をかくことに意味があるんだ。
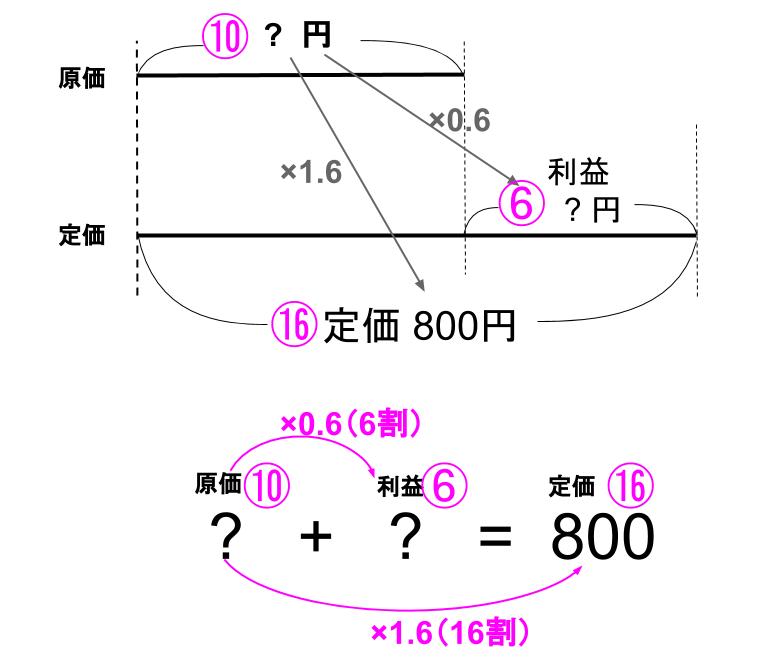

なるほど。
何についての話なのか正確にわからないと解けるわけがないですよね。

「6割増し」が「16割=1.6倍」であることだけを暗記していても解けないからね。
結局、八百屋さんが上のような足し算をしていることをきちんと想定していないといけない。

この状況が分かれば、
800÷1.6=500・・・原価
800-500=300・・・利益
とわかりますね。
求まりました。

うん。カンペキだよ。
とにかく商売の問題の基礎は、「特有の言葉の暗記」と「状況の理解」がすべてなんだ。
とにかく先生の教えたまとめ方で、完璧に解けるようになるまで練習してほしい。

別解もみせます。ぜひ理解してね。
上図でまとめた通りだけど、
⑯=800(円)なのだから、
800÷16=50
つまり、①=50
利益は⑥だから、⑥=300(円)
このように求めてもOKだ!
例題2
八百屋さんが、ぶどうに原価の4割の利益をつけて定価としました。このぶどうが1個売れると利益は140円となります。このぶどうの定価はいくらですか。
解説

原価の4割の利益をつけたのだから、「4割増し=14割=1.4倍」
140÷1.4=100
原価が100円なのかな・・・?定価は240円??

いやいや・・・大間違いだぞ。
問題文の状況をきちんと整理しましょう。
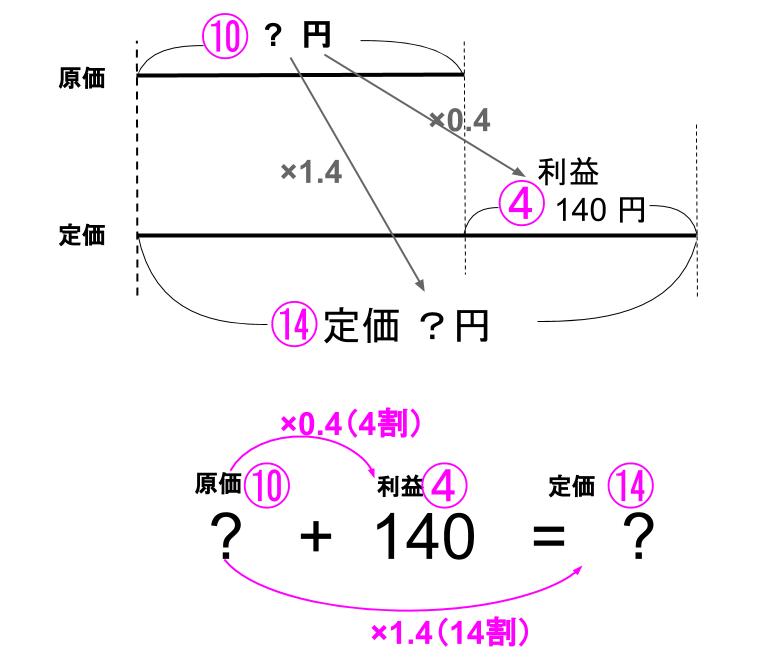

あ!140÷1.4=100なんてまるでダメダメですね・・・
原価×0.4=140
なんだ。
原価が逆算で求まるってことが目で見てわかります!
原価は、140÷0.4=350(円)
定価は、350+140=490(円)だ!

うん、この図のまとめかたをよく練習して、商売の状況を完璧に覚えてくださいね。

そして、別解もみせます。ぜひ理解してね。
上図でまとめた通りだけど、
④=140(円)なのだから、
140÷4=35
つまり、①=35
定価は⑭だから、⑭=35✕14=70✕7=490(円)
このように求めてもOKだ!
この図による情報整理は、いずれは省略することが目標です。
完璧に理解・暗記できたならば、毎度毎度この図を書く必要はありませんし、いちいち書かないでどんどん計算処理ができるようになるべきです。
実社会においては、定価から見て、原価がどれだけなのかを見ることが多い気がします。
ラーメン屋さんが、いかにして原価を抑えるかに苦心する。いわゆる原価率です。
このような視点で問題をつくることはもちろん可能ですが、中学受験算数において現在までに見かけたことはありません。まずは主流である、原価からみて利益は何倍か、という問題に慣れることが重要です。
もちろん与えられた文章をよく読んで、いわれたとおりに計算をしていくことが算数です。
原価をスタートとしない問題だって出題されうるので、非常に厳密な指導をするのならば、原価をスタート地点とする問題しかでないような誤解を与えてはいけません。
しかし、そこまで厳密な指導が有効な小学生はかなり優秀な一部の層だけだと思います。
まずは商売の世界にきちんと慣れること、割合の計算に習熟させること、を優先させましょう。
