1:商売の基本をマスターしよう
1 ふだん使わない商売特有の言葉を覚える。
2 比の感覚を鍛える。
あなたは商売をします。例えば八百屋さんの商売を想像してください。
自分が八百屋さんになったと思って、お金の動きを想像していくのです。

算数にでてくる商売はね、何かを仕入れて、それを高く売るってお話だよ。

100円のものを、500円で売るとか、そういうことですよね。

そうだね。
例えば、100円でリンゴを1個仕入れて、それを500円で売ったら、いくらもうかるかな?
ちょっと現実ではリンゴの値段としてはありえない金額だけどね。

400円かな?

そうだね。はじめ100円もっていて、その100円でリンゴを買って、
そのリンゴが500円で売れる。
きちんと商売の流れを理解しようね。
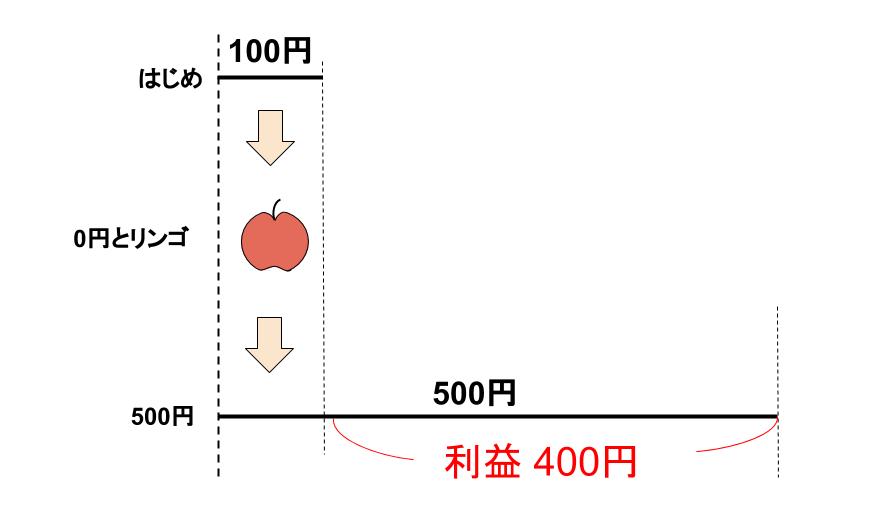

商売を通して、増えたお金のことを、「利益」とか「もうけ」と呼ぶよ。
こういう言葉はしっかりと覚えようね。
原価から定価へ

さて、毎度毎度リンゴの絵を書いてもいられないから、途中の図は省略していくよ。
まずは、商売特有の言葉を覚えることが大事。
またはじめから丁寧にやっていくよ。
そうだな、例えば、
ある八百屋さんが農家からメロンを500円で買って(仕入れて)、それを800円で売ることにする。
例えばの話だからさ、現実がいくらくらいなのかは知らないけども。
仕入れるための値段(500円)を、原価、または仕入れ値という。
次に、お客に売ると決めた値段(800円)を、定価というんだ。
とにかく言葉を知らないとどうにもならないからね、絶対に暗記しなくてはならないよ
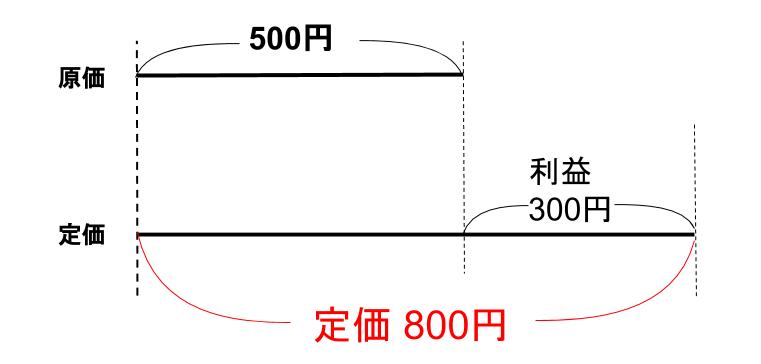

「定価」は、知らなくても問題文をきちんと読めば大丈夫なことが多いけど、算数の文章題の世界ではそれなりによく出てくるから、まあ知っておいてほしい。
「利益」、「もうけ」は300円だね。

さて、八百屋さんが定価をいくらにするか決めたときの状況を式にしてみるよ。
500円に300円を上乗せして売りたいと思うのだから、
これはつまり「足し算の式」になる。
まずこのあたりまえの全体像と、商売特有の言葉を覚えてね。


あれ?「割合」って「何倍」の話ですよね。
かけ算じゃないんですか?

そうだね。
「割合」とは、「AがBの何倍なのか」という話だよね。
今でてきた「原価」と「利益」と「定価」について、「何倍なのか」に着目していくからね。
算数で商売の話がでてきたとき、何と何を比べるのかはほぼ決まっています。
「原価に対して、定価は何倍なのか」
「原価に対して、利益は何倍なのか」
この2つ。
他のものを比べることは基本的にはないんだ。
例えば、
「定価は利益の何倍なのか」とか、
「原価は定価の何倍なのか」とか。
こういうものの見方をすることはない。
とにかく「原価からみて、他が何倍なのか」に着目する。
そして、商売では「歩合」を使うことが多いよ。
「百分率」も使うことがあるけどね。
下図のように理解すると良いでしょう。確認してみてください。
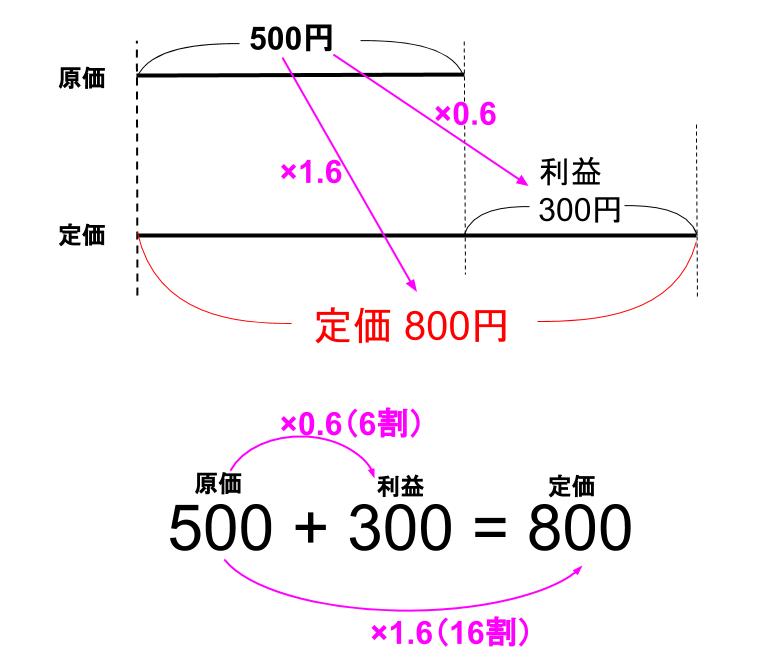

「原価に対して、定価は何倍なのか」
800÷500=1.6
定価は原価の1.6倍。
定価は原価の16割。
「原価に対して、利益は何倍なのか」
300÷500=0.6
利益は原価の0.6倍。
利益は原価の6割。
はい、大丈夫です。
~割り増し

さらに新しい言葉を確認をしておきたい。
「定価は原価の16割」
これを商売特有の言い回しで、
「定価は原価の6割増し」
と言うんだ。
2つは同じ意味の言葉なんだよ。
どうかな、同じ意味だってわかるかな?

「6割増し」と「16割」が同じ意味だってことですね。
えーーと・・・わかるような気もする?かな?

はっきりと「あたりまえ」とは思えていないね。
よし、説明していくからね。
まず、
原価は原価の何割かな?

え? えーーと・・・

原価は何倍すると原価になる?

原価×1=原価
1倍ですよね。

正解。だから、原価は原価の何割かな?

1倍=10割
だから、
原価は原価の10割です。

大正解!
今回の話は、「原価から見て定価が何倍なのか」だった。
割合において、何をスタート地点と見るのかはとても大事だよね。
今回の話のスタート地点は、原価。
すべて、原価からみて何倍なのか、という目で見ます。
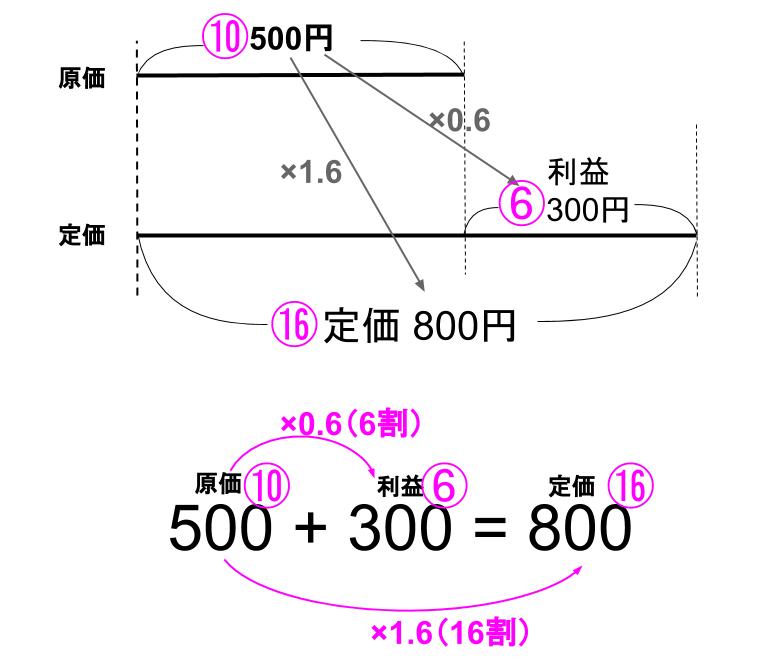

「定価は原価の16割」
とは、
原価10割に、利益6割を増して、定価16割にしているね。
つまり、
「原価の16割」と「原価の6割増し」は同じ意味である。
どう?わかってくれたかな。

そうですね。なるほど。
とにかく原価からみて、という視点ですね。

そう。「原価を10割」として話が進んでいることがほとんどだからね。
そして、
「定価は原価の16割」という言い方はまずしない。
「定価は原価の6割増し」という言い方をするんだ。
「定価は原価の6割増し」という言葉から、
(原価)×1.6=(定価)
ということだとすぐにわかるようになっておかないといけないよ。
