旅人算の標準レベル
例題6
1周720mの池の周りをAは分速90m、Bは分速30mで同じ場所から同時に同じ方向に進みました。AがBに追いつくのは出発から何分後ですか。
解説
出会いと違い、初見では考えにくい問題です。自力で答えにたどり着かなくとも問題ありません。

図をかいてみようと思うんですけど・・・
どうやってかいたらいいのか、ちょっとよくわからないなあ。

そうだね。
何分後くらいに追いつくのかな。検討はつくかな?
Aがどれくらい走ったところでBに追いつくのかな?

それがわかったら苦労しないです・・・ていうかそれを求めたいんですけど。

まあそうだよね。
正しい情報がないから正しい図がかけない。
だから、正しくない図でもいいからかいてみよう。
何もしないで固まっているよりはマシだよ。
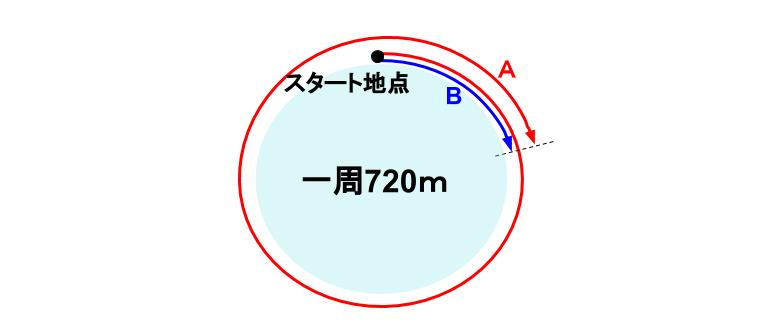
こんな図はどう?
AがBに追いつくってこういうことだ。

なるほど。こんな図になりそうかな。

で、どうしたらこの問題は解けるのかな?考えてみてね。

追いつきの旅人算なんだから・・・
2人の進んだ距離の差に注目かな・・・

うん、正解ですよ!AとBの進んだ距離の差はどうなってる?
図をよく見てごらん。

あ!わかった。
AがBより、1周分多く進んでます。

その通り!!
これが池をぐるぐる回る問題のポイントなんだよ。
速い方が、遅い方に、1周差をつけたときに追いつく。
きちんと理解した上で、必ず暗記してください。
では、問題の答えを出そう。

1周は720m
90-30=60・・・AとBの1分で進む距離の差
720÷60=12
12分で追いつきます!

正解!
正しい数値をもとに、正しい図をかいてみようか。
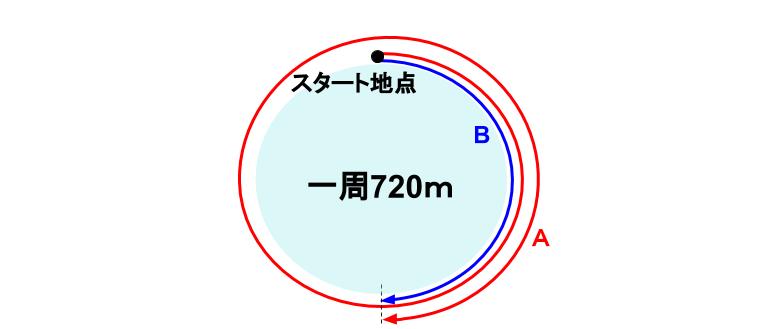
Aは12分で、90×12=1080m進む。
1周が720mだから、
Aは720m+360m進んだ。
つまり、Aは1周半進んだ。
Bは、30×12=360m
つまり、Bは半周進んだ。
下図のようになっているということですね。

なるほど。うまくいってますね。
別の視点から考える

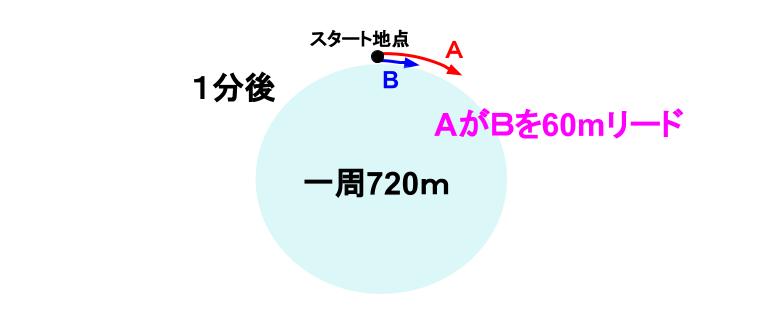
ところでね。さっきの問題なんだけど、2人がスタートしてから1分後の図は簡単にかけるね。
AがBより、60m先を進んでいるわけだけど。

これから何分後に、AがBに追いつくのか考えてみて。

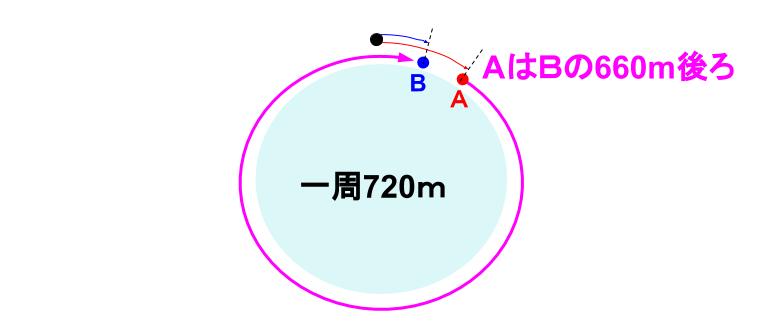
720-60=660m
AはBに、720-60=660mリードされているとも見えますね。
AはBに対して1分ごとに、90-30=60mずつ差をつめていくから、
660÷60=11
11分後に追いつきます。

うん、「スタートから1分後」から旅人算をはじめて、11分で追いつくのだから、1+11=12、スタートから12分で追いつく。
もちろん先ほどと同じ答えがでたわけです。

この解き方なら、「速い方が、遅い方に、1周差をつけたときに追いつく」って覚えてなくても解けますね

うん、そうなんだけど、「速い方が、遅い方に、1周差をつけたときに追いつく」は基本中の基本事項として必ず覚えてね。
覚えていないで上のように解くと、2段階で解かなきゃいけないからね。
で、なんでこんな解き方を持ち出したのかいうと・・・
スタートから1秒後のことを考えてみて欲しい。
AはBに対して、ほんの数cmだけリードしている。
見方を変えれば、
AはBに対して、「1周720m-ほんの数cm」を追いつかなくてはならない。
では次に、スタートから0.01秒後のことを考えてみて欲しい。
スタートから0.000001秒後のことを考えてみて欲しい。

スタートから0.000001秒後か。
AはBに対して「ほぼ1周分リードされている」ようなものですね。
だから、「速い方が、遅い方に、1周差をつけたときに追いつく」なんだ。

うん、そういうことだよ!
図示することの難しさ

ところで・・・
Aが分速70m、Bが分速50m。
この2人が池をぐるぐる回るとしよう。
池一周は700mとする。
AはBになかなか追いつけないよね。
速さの差が小さいからね。
何周も何周もぐるぐる回ってようやく追いつくことになる。
これを正しく図示してもめちゃくちゃな図になって、何がポイントなのか良くわからない。
とりあえず計算してみると、
700÷(70-50)=35分
Aは70×35=2450m進んだところで追いつく。
これは、2450÷700=3.5だから、Aが3周半したときに追いつく。
Bはその間に、50×35=1750m、2周半進む。
確かに1周差をつけられたところで追いつかれているね。
で、この状況を正しく図示してみると・・・
ぐちゃぐちゃになって何がなんだかまったくわからないことになる。
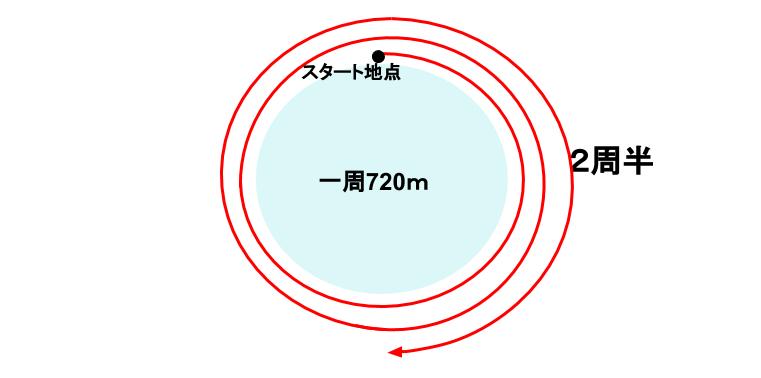
例えばBが池を2周半した図が下図。
この段階ですでに何周したのか、一瞬ではわからないね。

目がまわります。

この図とAが池を3周半した図を並べたり、重ねて図をかいたり・・・
ぐちゃぐちゃの図にぐちゃぐちゃの図を合わせて。もうまったくお手上げになる。
だから、「速い方が、遅い方に、1周差をつけたときに追いつく」を覚えなくとも、毎回図をかけば導き出せる!というのはちょっと現実的でない。
池をぐるぐる回る問題の図は、このようになることがあるからね。
だからこそ、
「速い方が、遅い方に、1周差をつけたときに追いつく。」
というポイントは、理解した上で暗記しておかないといけない。
サラッと計算だけで答えを出せるようになっておいて欲しい。
「原理や考え方さえ押さえておけば公式暗記はいらない、テストの現場で導いてしまえばいい」は、通用しにくいものだってあるのです。