例題4
Aは分速90mでP地点からQ地点へ、Bは分速60mでQ地点からP地点へ同時に出発しました。PQ間の距離は1800mです。
(1)2人がはじめて出会うのは、出発から何分後ですか。
(2)AはQ地点に着くと同時にP地点へ折り返し、BはP地点に着くと同時にQ地点へ折り返しました。2人が2度目に出会うのは、出発から何分後ですか。
解説
例題1・2・3と同様に、全く何も教えずにやらせて、子どもが自力で解けて欲しい問題です。
(1)2人がはじめて出会うのは、出発から何分後ですか。

これは、なんのひねりもない出会いの旅人算ですね。
1800÷(90+60)=12分
12分後ですね。

うん。正解
図がどのようになるかが完璧に頭の中に描けるのならば、図をかかないで求めてしまって良いよ。
それに、それくらいのレベルに達していないのならば、ここから先を練習するよりも、前にもどって基礎固めをした方がいいぞ。
(2)2人が2度目に出会うのは、出発から何分後ですか。

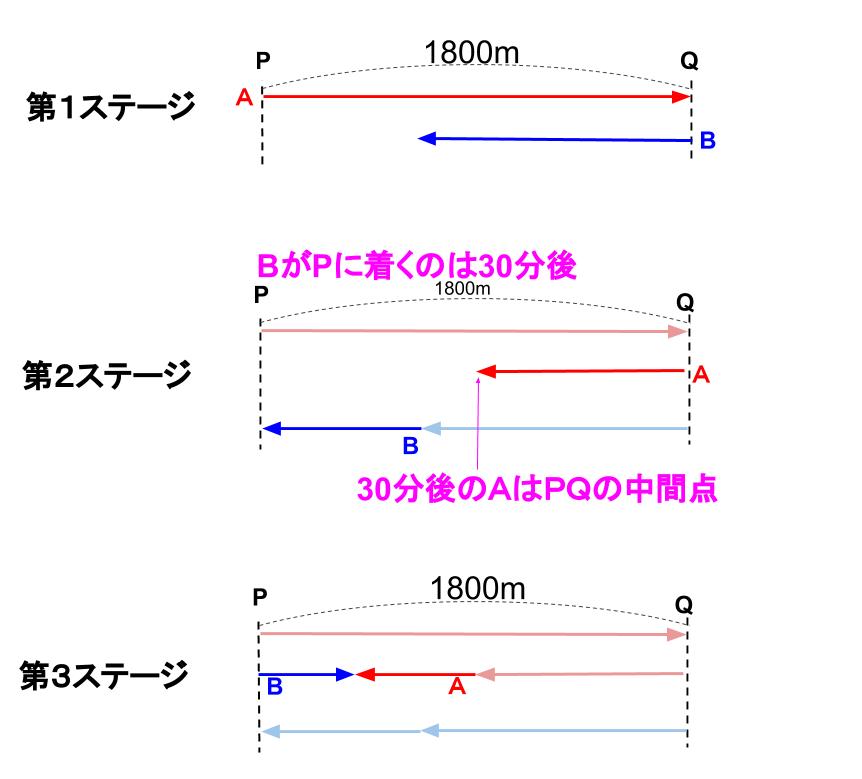
1.まず Aが折り返す
2.次にBが折り返す
3.AとBが2度目の出会い
3段階の問題ですね。

うん、AとBの動きを上手にとらえているね。
あとは、第3ステージの出会いの旅人算の計算をすれば正解だね。

Bが折り返す30分後、AとBの間の距離は、900m。
この後、Aは分速90mでBは分速60mで、向かい合って進むから、
900÷(90+60)=6
つまり、30+6=36
36分後に出会います。

正解です。素晴らしいですね。
ところで、
3段階に分けないで1段階で解けるんだけど、考えてみて。

あ!さっきの例題3とそっくりに考えるのか。
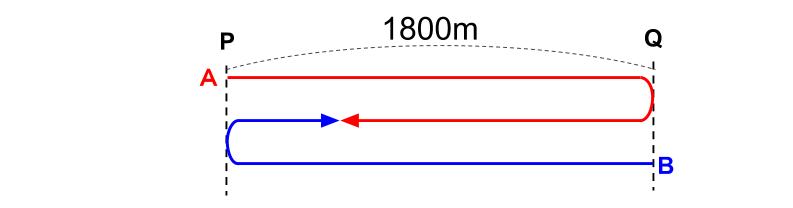
スタートから2度目の出会いまで、ずーっと2人は同じ速さだから・・・
進む向きを変えても気にせずにひとまとめにしよう!

2人の進んだ距離の合計が、PQ間の距離の3倍になっています!
PQ間の距離は1800m
1800×3=5400・・・2人の進んだ距離の合計
90+60=150m・・・2人が1分で進む距離の合計
5400÷150=36分
答えは36分です。2人が2度目の出会いをするのは出発から36分後です。

お見事!先ほどの例題で学んだことを活かせたね!
はじめに、3段階にわけて図示することは無駄ではありません。
いきなり1段階の図を見せても、「わかったつもり」になるだけです。
問題が変わり、数値設定が変われば、図も変わるからです。
ちなみに、途中AがBを追い抜くことはないのでしょうか?
AとBの速さに大きな差があれば、AはBがPに着く前に追いこします。
このような問題ももちろん存在します。