例題3
Aの歩く速さは分速50m、Bの歩く速さは分速40mです。2人はP駅を午前9時に出発して、1800mはなれたQ公園に向かいました。AはQ公園に着くとただちに引きかえしました。2人が出会うのは、何時何分ですか。
また2人が出会ったのは、P駅から何mはなれたところですか。
解説
例題1・2と同様に、全く何も教えずにやらせて、子どもが自力で解けて欲しい問題です。

これも2段階ですね。

何と何の2段階かな?

AがQに着くまでがステージ1です。
AとBが同じ方向に進み、速いAが遅いBに差を広げていきます。
次に、Aが折り返してからがステージ2です。
AとBが向かい合わせで進み、どんどん近づいていって、そして出会います!

素晴らしいね。じゃあ解いちゃってください!

1800÷50=36
36分でAはQ公園に着きます。
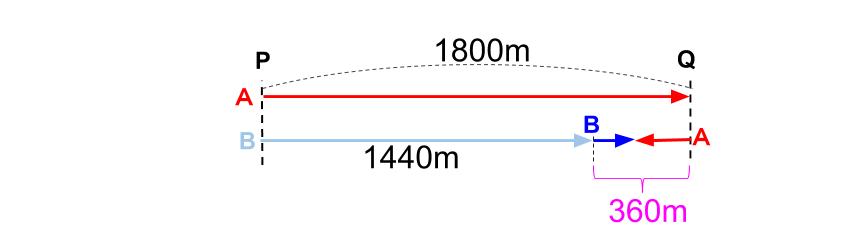
そのとき、Bは、40×36=1440m進んでいます。

で、Aが折り返す。ステージ2になります。
AとBの出会いの旅人算だ。
2人の間の距離は、
1800-1440=360より360m
2人は向かい合わせで1分に、50+40=90mずつ近づくから、
360÷90=4
4分で出会う。
午前9時の36分後の4分後に出会ったのだから、答えは午前9時40分!

素晴らしい。正解です。
2人が出会ったのは、P駅から何mかな?

B君が進んだ距離を求めればいいですね。図をみれば明らかです。
Bは、36+4=40分間進んだから、
40×40=1600m
出会った場所は、P駅から1600mです。

大正解!言うことなし。
図を見ながら解くと、次に何を求めればよいか、迷いにくくなるよね!

ところで、これが自力で解ける子には、先生からプレゼントを送るんだ。
自力で解けない子にはまだあげられない特別モノだ。
例題3の追加プレゼント問題
この例題3を、1段階で解く方法がある。
どうすれば良いか考えてください。

??プレゼントって・・・問題なの?
しかも・・・難しいんですけど・・・

そうだね、難しいよね。だからヒントをあげるね。
1段階で解くということは、「スタートからゴールまでをひとまとめで見る」ってことだよ。

はあ、そうですね・・・

さっき、Bの動きをひとまとめで見たってわかる?
第1ステージの36分間と第2ステージの4分間をわけないで、Bの動きをスタートから40分間のひとまとめにして見たよね。
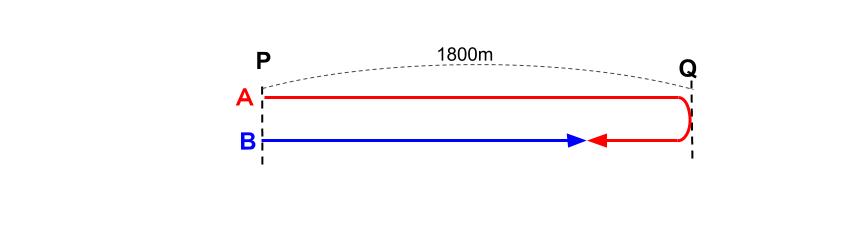
同じように、Aの動きもひとまとめにして図示してごらん。

こんな図かな?

OK。素晴らしい。
この図で、解けるよ!

?わからないです・・・

「2人の進んだ距離の和」か「2人の進んだ距離の差」に着目するしかなさそうでしょ。

あ!!
2人はスタートから出会うまでに、合計で、1800×2=3600m進んだ。
2人は1分で合計、50+40=90
より、90m進むから、
3600÷(50+40)=40分
40分後に出会ったんだ!

お見事!!!ばっちり正解だよ!!
これで先ほどと同じ結論にたどり着くわけだね。
見方を変えれば、はじめ2人は3600m離れていたようなものだ。

えーっ。どんな見方ですか?
はじめ、AとBは同じP駅にいますよ。

例えば、Aは2階、Bは1階にいた。
Q地点でAは1階に下りて、Bの方に向かった
とかね。

おおっ・・・なるほど!
この問題を自力で取り組んだ場合、ほとんどは2段階での解法を取ると思います。
これで解けた子はとても素晴らしいです。1段階の解法が思いつかなくても全然問題ありません。
そして、より上手な解き方、1段階で解く解法を知ることで、より算数に興味がわくのです。
何も考えさせないうちから、いきなりうまいやり方を教えても、工夫することや、違う視点のおもしろさが失われてしまいます。