1:旅人算のいろいろ
2段階の動き
例題1
Aの歩く速さは分速70m、Bの歩く速さは分速50mです。Bが午後5時に公園を出発し、その4分後にAが同じ公園を出発してBを追いかけました。AがBに追いつくのは何時何分ですか。
解説
全く何も教えずにやらせて、自力で解けて欲しい問題です。
図示も何もせず、解けない解けないと言うようでは、算数の学習とは何なのかまだわからない状態です。
そういう子にとっては、習った公式にあてはめて計算する科目が算数という認識なのでしょう。
ゆっくりじっくり、図をかいて考えていく姿勢を身につけていきましょう。
特に新しく教えることはない、もうすでにこの問題を解くために知識は教えてあるよ、といって1人立ちさせてください。3分くらいまったく手が動かずに白紙ならば、
2人の動いている様子を図にするように声かけをします。
それでも手が動かないなら、5時1分の絵をかかせ、5時2分の絵をかかせ、5時3分、5時4分・・・とわかるまでかかせます。
この問題を理解したといえる到達地点は、2人の間の距離の変化が、2段階であると理解することです。

えーと、旅人算は和か差のどちらかだったから・・・・
えーっと。

「旅人算は和か差のどちらかに着目」っていう事実は暗記でよいけども、
問題を解く姿勢としてはよくないな。大間違いですよ。

?

どんな問題にもいえることだけど、問題の状況をきちんと理解すること、そのために整理したり図示したりすることを第一にやるべきだよ。
そもそもこの問題は旅人算なのかな?
旅人算なら、「旅人算は和か差のどちらかに着目」っていう頭になってもいいけど。

え?旅人算なのかどうかって・・・AとBの2人が動いているし、旅人算じゃないんですか?

旅人算じゃない、とは言っていないよ。
とにかく問題を図にしてみて、状況を理解しようよ。

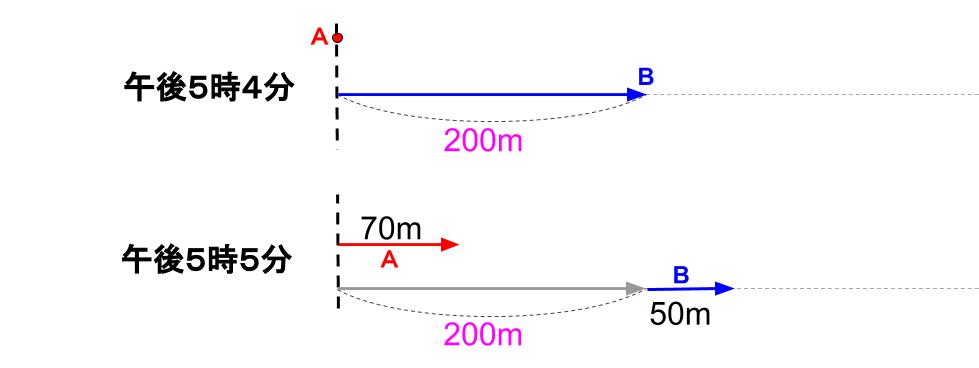
まずBが出発。4分後にAが出発すると、・・・
Bが分速50mで4分進んだ距離は、50×4=200(m)だから、
午後5時4分は、こんな図ですね。
そして、さらに1分たった図もかきます。

とても上手な図ですね。
速さの図は必ず、動いている最中のことを考えながらかくんだよ。
午後5時4分から先は、2人が同時に動いているよね。
その2人が動いていって・・・どうなる?
2人の間の距離は縮まるの?広がっていくの?

あ、ここが旅人算なんだ!
2人の間の距離が、どんどん縮まっていって追いつくんだ。
ということは、1分にどれだけ差が縮まるかが分かればいい。
2人の進んだ距離の差だから、
70-50=20(m)
1分で20mずつ縮まる。
200mの差が縮まるのは10分だ。

OK!
で、なんて答えるのかな?

午後5時10分かな。

それは間違い。
最後の計算で求まった10分は、何が求まったのかよく考えてね。

200mの差がつまるのに10分かかりました。

その通り。
つまり、2人の追いかけっこがスタートしてから、差が0になるまでに10分かかるということだよね。

5時4分から追いかけっこがスタートしたから、追いついたのは5時14分だ。

正解!
時間の10分と時刻の10分は、ごちゃ混ぜになっている子はとても多いよ。
注意して区別しないといけないと覚えておいてね。
この問題は、
Aは5時4分から5時14分までの10分間で、700m進んだ。
Bは5時0分から5時14分までの14分間で、700m進んだ。
という状況だったのです。
時間とは幅のある期間のこと、時刻とは点のことです。ごちゃまぜになっている子どもはとても多いので、よく説明してあげましょう。