1:旅人算やや応用
真ん中で出会う・その1
例題3
Aは学校から公園に向かって午前9時に出発しました。Bは公園から学校に向かって、午前9時3分に出発しました。2人は学校と公園のちょうど真ん中のP地点で出会いました。Aは分速75m、Bは分速100mのとき、学校から公園までの距離を求めなさい。
解説

とにかく図示ですね!
えーーと、これは2段階ですね。

うん。まずは第1関門突破だね。

第1ステージ
はじめの3分間は、Aだけが動いてます。
第2ステージ
その後、AとBが出会いの旅人算です。
下図のようになりますね。
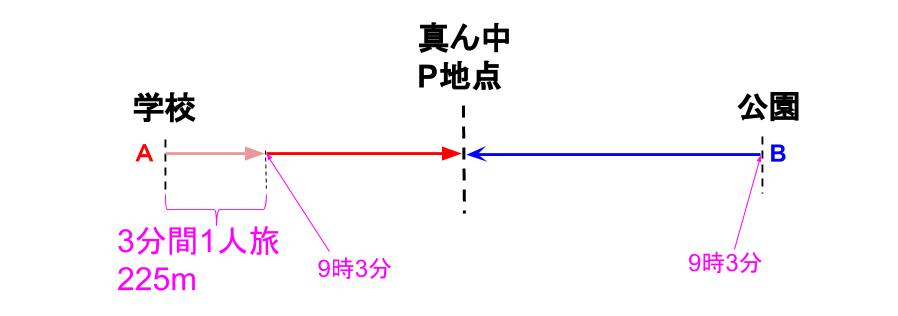

で・・・次が分からないな・・・

今までやってきたことは限られているよ。どれを使えばいいか考えるんだよ。

えーーー!和差算じゃないし。つるかめ算・・・?

ちゃんと考えてますか?
さすがにつるかめ算じゃないってすぐにわかってね。
2人が、9時3分から出会うまで、ヨーイ・ドンで進んでるんだよ。

旅人算です・・・よね?

そう。旅人算だ。旅人算は大きくわけると2パターンだ。
何と何だった?

「出会い」と「追いつき」かな。

30点かな。間違いとは言わないけど、それではこの問題は解けない。
旅人算は、「2人の進んだ距離の和」に着目するか、「2人の進んだ距離の差」に着目するか。この2パターンだ。
改めて覚えなおしてください。

はい。
ということは・・・今回は・・・「出会い」だから「和」な気がするんだけど・・・


和だと、「225m」に結びつかないでしょ。
今回は「2人の進んだ距離の差」に着目してごらん。

あ!「2人の進んだ距離の差」が225mだ!!
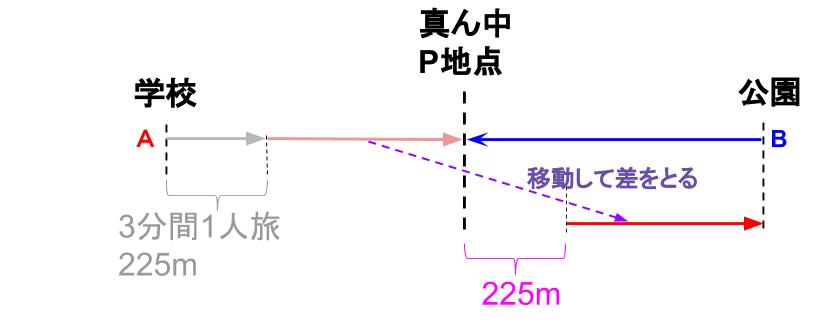

ああ、そういうことか。あとは計算するだけですね。
Aが分速75m
Bが分速100m
2人の進んだ距離の差が225mになるのは、
225÷(100-75)=9(分)
Bが9分で進んだ距離の2倍が、学校から公園までの距離だから、
100×9×2=1800m

正解です。
確かめをしておこうか。
Aは、3+9=12分かけて、真ん中まで進んだから、
75×12×2=1800m
BでだしてもAでだしても同じ答え、矛盾がないね!
なかなか難しくなってきたね。基本が完璧に身についていないようなら、前に戻って基礎固めをしてからにしようね。
