速さの基礎文章題
途中で速さを変える
例題1
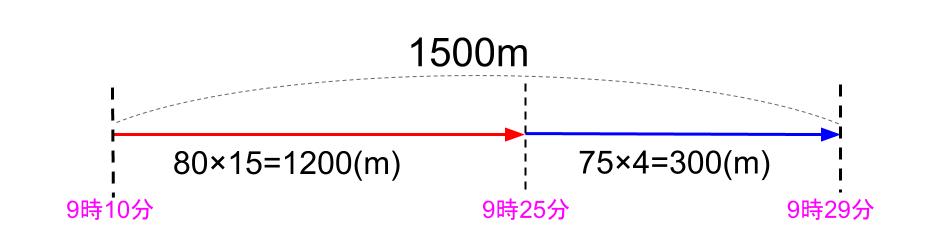
家から駅まで1500mあります。9時10分に家を出発し、分速80mの速さで駅に向かいました。9時25分に速さを分速75mにかえました。駅に着いたのは何時何分ですか。
解説

9時10分から9時25分までの15分で進んだ距離は、
80×15=1200(m)
残り300mを分速75mで進んだから、
300÷75=4
4分かかる。
9時25分の4分後の9時29分に駅に着いた。
答えは9時29分です。

正解です!
例題2
つぎの□にあてはまる値を求めなさい。
家から駅まで、分速72mで35分かけて進み、帰りは、分速45mで□分かけて帰った。
解説

家から駅までの距離は、72×35=2520m
帰りは2520mを45分で進んだ。
2520÷45=\(\displaystyle \frac{2520}{45}\)
まず5で約分します。
\(\displaystyle \frac{2520}{45}=\displaystyle \frac{504}{9}\)
あ!割り切れそうですね。
\(\displaystyle \frac{504}{9}\)=56
56分です!

正解なんだけど、計算はちょっと下手だね。
もっと計算上手になろう。
そもそも、この問題において、家から駅までの距離は計算する必要はないよね。
家から駅までの距離は、72×35m
これで十分。
72×35の計算結果がいくつになるのかは求める必要はない。

え?そうなの??

だって、聞かれてないでしょ。
家から駅までの距離は何mですか?って問われれば、72×35を計算して、2520mと答えなくてはいけないけれどね。
今回は、この距離を分速45mで何分かかるのか、これが聞かれている。
だから、(72×35)÷45を計算すればよい。
もちろん、すぐに分数にする。
(72×35)÷45=\(\displaystyle \frac{72×35}{45}\)
もちろん約分をしていくのですよ。

なるほど!
こっちの方が約分しやすいし、計算も楽ですね。
9や5で約分できることもすぐにわかります。

そういうことです。
便利でしょ。
なんでもかんでもすぐに計算するのではなく、計算を途中でやめておくことで、続きの計算(約分)が楽になることが多いよ。
これは他の単元でも有効な計算テクニックだから、常に意識して学習に臨んでくださいね。
