1:速さの基本をマスターしよう
速さを極めよう。
1:時間と距離が正比例
時速とは何か、速さについて話をしてみてはいがかでしょうか。
また人の歩く速さはどれくらいでしょうか。
「速さ」について親しんでおくと良いでしょう。
例題1
太郎くんは50m走をしたところ、スタートからゴールまで10秒かかりました。
太郎くんは100m走るのに何秒かかりますか。
解説

今日は「速さ」だよ。算数の主役といってもいい単元だよ。

ふーん、ところで、太郎くんは疲れないんですか?

うん疲れないよ。
算数の世界では、特にただし書きがない限りは、ロボットのようにずっと同じ速さで動くよ。

なんか変なのー

ロボットじゃないとたいへんだぞ。
難しすぎて解けないよ。
ずーっと一定の速さで動くありがたみをかみしめてくださいな。
算数という架空の世界では太郎くんは、常に一定の速さで走ります。こういうお約束に疑問を持つ子どもには、「算数はパズルだから、一定の速さで走るのが暗黙のルール」と教えてあげてください。

確かにそうですね。
例題を解きますよ。
50mを10秒の太郎君は、100mを20秒です。
簡単、簡単。暗算で一発です!

考え方は?どうやって解いたのかな?

だって、50m走ったあとにさらに50m走ると100mになるんだから、
10秒走ってさらにあと10秒走るわけでしょ。全部で20秒だよ

うん、正解。
下の図のようになっているよね。


では、太郎君は3秒でどれだけの距離を走りますか。

う・・・えーっと。

じゃあ、太郎は1秒でどれだけ走るかな?

太郎くんは50mを10秒だから、
1秒で5m走る。
ということは、
2秒で10m
3秒で15mだ。

うん正解だよ。簡単だったかな?
でも改めてきちんと、目で見て確認しておきたい。
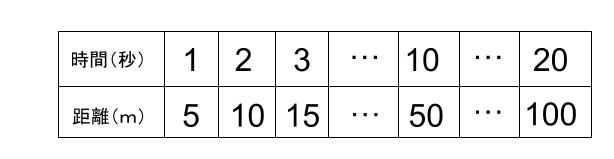
何も教えないで解いてもらったけども、下の表が成り立つっていうことが、この問題を解くためのカギだね。
どうかな、これはあたりまえだって思えるかな?

あたりまえだよ。だってずっと一定の速さだって確認したもの。

OK!
この仕組みさえ理解しておけば、「速さ」の学習の大部分は終了なんだよ。
速さは「この表がすべてだ」と言ってもいい。
時間が2倍になれば、進む距離も2倍になる、
時間が3倍になれば、進む距離も3倍になる、
この関係は、
1個20円のアメが、2個40円、3個60円・・・になるのとまったく同じ関係だね。
このような関係を「正比例」というんだ。この言葉は忘れてもいいけど、
小学生が算数で扱う内容は「正比例ばかり」である、ということは意識しておいた方がいいかもね。

え? 簡単すぎてびっくり!
算数の主役ってこんなに簡単なの!?

さすがにこれほど単純なものばかりではないけれどね。
でもどんな難問も、突き詰めればこの仕組みだっていうことは間違いない。
それにね、「わかった」のさらに先「すらすら使いこなせる」のレベルに到達してもらわないといけない。その練習はそんなに楽じゃないかもね。
いわゆる「速さの3公式」から導入してはいけません。公式を教えると、本質的な理解をしようとしない子どもがいます(公式を覚えて、それを適用した計算をすることが大事なことと思う子どもがいます)。
※アメは1個、2個・・・と個数が整数にしかなりません。
速さでは1.5秒とか、0.1秒とか整数でない値も考えていきます。
そういう意味では、水と重さの関係の方がより適切かもしれません。
1L1000gの水が2L2000g、3L3000g・・・ 0.1Lで100gと比例します。
※正比例の表を書いて解いていくうちに、表はかかなくても解けるようになります。
表を書かなくても瞬時に計算ができるようになるまで練習しましょう。
