通過算と比
通過算と比
例題1
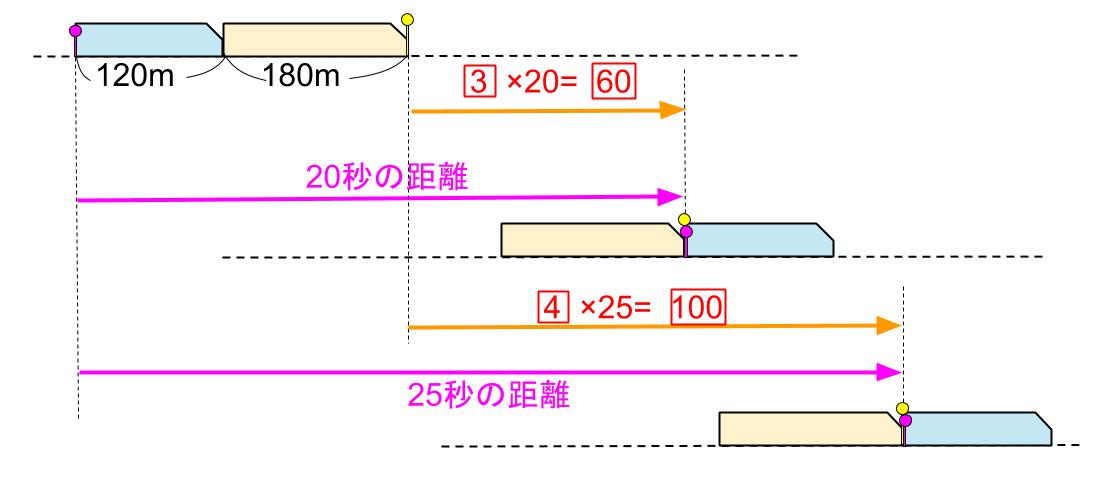
長さ180mの貨物列車に長さ120mの急行列車が追いついてから追いこすまでに20秒かかりました。もし、貨物列車の速さが \(\displaystyle \frac{1}{3}\) だけ速かったならば、急行列車がこれを追いこすのに、25秒かかるはずです。両列車の速さはそれぞれ秒速何mですか。
解説

線分図で解くか、式処理で解くか。
両方の解き方を見てみようと思っています。

式にして、比を活用すると楽なんですよね。
式処理でやってみます。
(速さ)×(時間)=(距離)
(急行の秒速ー貨物の秒速)×20=(180+120)
(急行の秒速ーもしもの貨物の秒速)×25=(180+120)

\(\displaystyle \frac{1}{3}\) だけ速かった
というのは比の情報だよね。

3:4ですね。
貨物の本当の速さが③
もしもの貨物の速さが④とおけますね。
(急行の秒速ー貨物の秒速③)×20=(180+120)
(急行の秒速ー貨物の秒速④)×25=(180+120)

そうだね。
ここまできたら、後は計算するだけだよ!

(急行の秒速ー貨物の秒速③)×20=(180+120)
なのだから、300÷20=15
つまり、(急行の秒速ー貨物の秒速③)=15
また、
(急行の秒速ー貨物の秒速④)×25=(180+120)
なのだから、300÷25=12
つまり、(急行の秒速ー貨物の秒速④)=12
いまわかった2つを見比べる・・・
(急行の秒速ー貨物の秒速③)=15
(急行の秒速ー貨物の秒速④)=12
③引いて15だけど、さらに①ひくと12になる。
つまり、①=3
貨物の秒速③=9
急行の秒速は、9+15=24
求まりました。
貨物は秒速9m
急行は秒速24m

はい。正解です。
とても上手に式処理ができましたね!
別解・線分図

さて、線分図で解くとどのようになるのか一度経験してもらった方が良いと思う。
線分図をかいてみてください。

はい。やってみます。
えっと・・・大変ですね、これは。

この図をかける子はほんの一握り。
ほとんどの子はかけない。
それに、図をかけてもその後の処理までやりきれる子はさらに少なくなる。
式処理の方が圧倒的に楽に解けることが分かってくれたと思う。

そうですね。
この図は無理かな・・・

ちなみに、この後どうやって解くのかについて一応説明はしておくよ。
線分図の差をみることで、
急行が5秒で動く距離=40
だから、
急行が20秒で動く距離=160
より、300m=160-60
つまり、1=3
なので、貨物の秒速は3=9
こんな流れです。

今見てきたとおりなんだけど、4つのものが動くから、4本の線分図をかかないといけない。
そして、それの差をとって・・・
かなり大変だよね。
式処理でさらっと解けるようになっておくことおススメなんだよ。

あとね。ちょっと豆知識。
線分図で解いてもそれほどつらくない問題だってある。
それはどんな問題かというと、線分図を2つしかかかなくて済む問題。
例えば、ある電車がトンネルPとトンネルQを通過するときを比べる問題。
トンネルは動かないから、2つの線分図を比べるだけで解けます。
一つ前のページで扱ったよう問題だね。
あと、4つの線分図をかく問題でも、人や車のように点として扱えるものが動く問題ならば、上の例題よりは楽に解けるよ。
何はともあれ、どのタイプの問題も式処理すればほとんど同じくらい簡単に解けるからね。
式処理がおすすめです。

では通過算は、もう式処理だけで解いていけば良い?

まあ、それで済む子が多いのも事実。
ひねった通過算を解けるようにならなくてもいいならば、式処理だけで済む。
しかし、難しい通過算になれば、図示は必要だからね。