通過算と比
通過算と比
例題1
ある電車が180mの鉄橋を渡り始めてから渡り終わるまでに16秒かかり、300mのトンネルに入り始めてから出終わるまでに22秒かかりました。この電車の長さは何mですか。またこの電車の速さは時速何kmですか。
解説

ここからは、「通過算と比」を学んでいきましょう。
以前、2つの線分図をかいて、差をとって解いた問題です。
今でもちゃんと解けますよね?

解いてみますね。
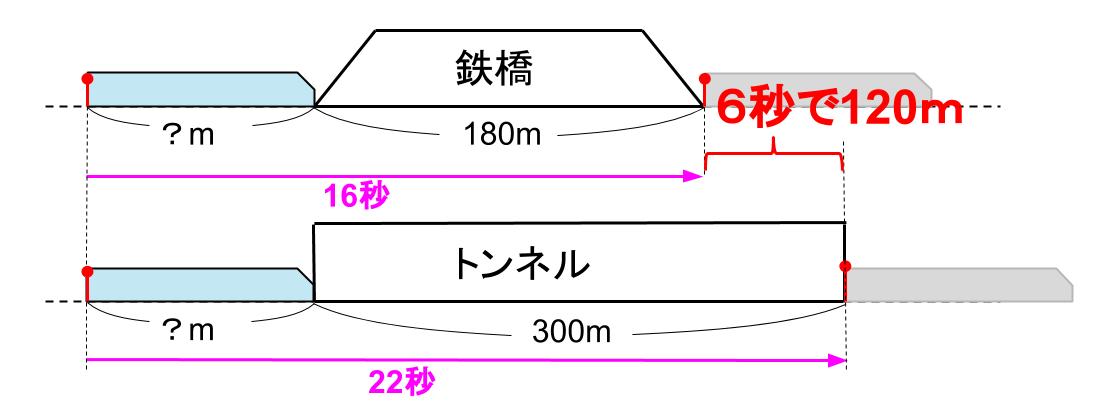
こんな図ですね。

6秒で120mだから、秒速20m、これが電車の速さ。
16秒で320m進むから、320-180=140
電車の長さは140m
大丈夫です。解けました。
正解ですよね?

はい、正解です。
今日はこの問題の、比を用いた別解を学習します。
ここから「通過算と比」はスタートします!

この問題では、2つの通過についてかかれていますね。
それぞれを式で表してみましょう。
どのような式になるかが瞬時にわからないならば、もちろん通過算の図をかいて確認するんですよ。
そして、通過算の基礎に戻って練習すべきです。「比の利用」の学習をする前に、基礎固めをしっかりやっておくべきだよ。

通過算の基礎はばっちりですよ!
(距離)÷(速さ)=(時間)
(180+電車の長さ)÷(電車の速さ)=16秒
(300+電車の長さ)÷(電車の速さ)=22秒
となりますね。

うんOK!
もちろん
(速さ)×(時間)=(距離)
(電車の速さ)×16秒=(180+電車の長さ)
(電車の速さ)×22秒=(300+電車の長さ)
でもOKだ。どちらも同じことを表している式だよね。
6÷2=3と2×3=6が同じなのと一緒です。
どちらで解いてもいいけど、今回は
(速さ)×(時間)=(距離)
(電車の速さ)×16秒=(180+電車の長さ)
(電車の速さ)×22秒=(300+電車の長さ)
で解きましょうかね。
あとはこの2つの式を比べることで答えをだすことができます。

比をとるんですよね・・・
速さの比は・・・1:1
同じ電車が同じ速さで進んでいるから。
時間は分かっているから、距離の比が計算できます。
つまり、
(速さ)×(時間)=(距離)
電車の速さ①×16秒=⑯(180+電車の長さ)
電車の速さ①×22秒=㉒(300+電車の長さ)
です。

そういうことです。
あとは計算するだけで答えが出るからね。
やってみてね。

⑯=(180+電車の長さ)
㉒=(300+電車の長さ)
がわかった。2つの式の差をとれば、
⑥=120
6で割って、
①=20
つまり、電車の速さが秒速20mということ。
そして、⑯=320=(180+電車の長さ)
より、電車の長さは140m
求まりました!

大正解!
比を活用することで、式処理だけで解くことができたね。
以前は線分図で解いた問題なのだけど、この式処理の解き方もどんどんできるようになって欲しいのです。

なぜですか?

線分図で解くとかなりつらい問題があるからなんだ。
でも、比を使って式処理すれば簡単。
そういう問題があるんです。
次のページでそんな問題をやりましょう。