流水算と比の利用
流水算と比の利用
例題1
ある川の上流にA地点、下流にB地点があります。船PがAからBへ、船QがBからAへ同時に出発しました。2つの船は出発から8分後にすれ違い、その4分後に船PはBに着きました。船QがBからAへ上るのにかかる時間は何分ですか。
解説

さて、「流水算と比」について学習していきましょう。

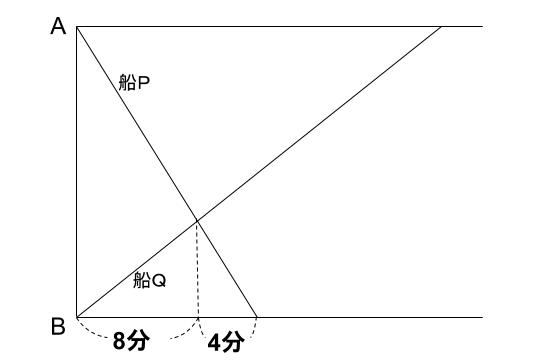
はい。では、ダイヤグラムにまとめてみますね。

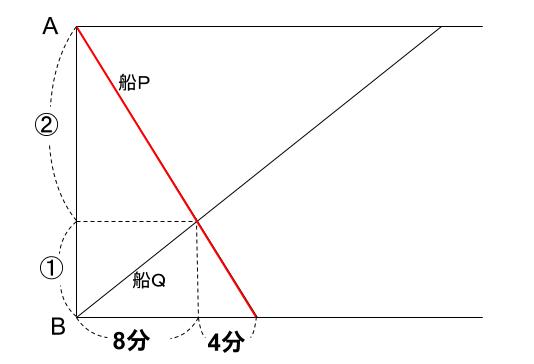
船Pに着目します。
8分で進む距離と4分で進む距離の比は、8:4=2:1

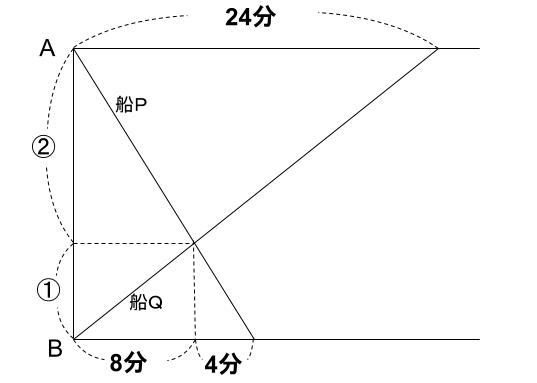
次に、船Qに着目します。
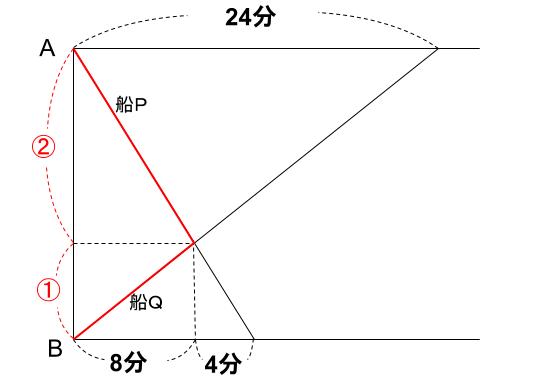
船Qは、①を進むのに8分かかったから、あと②進むのにかかる時間は16分
より、船Qは、8+16=24
24分かかってBからAまで上りました。

正解!
ところでさ、この問題は「流水算」だった?

川を船が上ったり下ったりしてるんだから、「流水算」でしょ。

あらためて問題を読み直してごらん。
川と船ではなくて、学校から駅までをPくんとQくんが進む問題でもいいのではないかな?

ああ、言われてみれば。

つまり、「流速」に関する考察をしない限り、ただの「速さ」の問題なんですよ。
川だろうが船だろうがね。

なるほど。そうですね。

かなり大事なことを言いました。
とても大事なので、くりかえしておきますね。
「流水算」も、普通の「速さ」の問題と同じなのです。
基本的な構造はまったく変わらない。
その構造とは、「速さ×時間=距離」のことです。
そして、その比の活用です。
今回は、船Pに関して、
(速さ)×(時間)=(距離)
1×8分=②
1×4分=①
という比の利用をしましたね。

はい。
「流速」とか「静水時の速さ」とか、まったくでてきませんでした。

「流速」とか「静水時の速さ」とかは、
(速さ)×(時間)=(距離)という主役の構造の中の、
「速さ」の部分にオマケがついているだけなのです。
それが流水算と呼ばれているもの。とにかく主役は、今まで通りの「速さと比」なんですよ。

はい。
わっかりましたあ!
例題2
ある川の上流にA地点、下流にB地点があります。船PがAからBへ、船QがBからAへ同時に出発しました。2つの船は出発から8分後にすれ違い、その4分後に船PはBに着きました。船PとQの静水時の速さは、どちらも分速75mです。この川の流れの速さは分速何mか求めなさい。
解説

「静水時の速さ」と「流速」がでてきましたね!

うん。
それ以外は、さっき解いた例題と完全に同じです。
「船PとQの静水時の速さは、どちらも分速75m」という情報が追加されただけ。

そうですね。
同じように解きます。下図のようになりますね。

で、今回は、「静水時の速さ」と「流速」の話が追加されているわけですよ。
「上りの速さ」=「静水時の速さ」-「流速」
「下りの速さ」=「静水時の速さ」+「流速」
あとは、これで解くわけです。

船P、Qはどちらも静水時が分速75mですね。
「上りの速さ」=75-「流速」
「下りの速さ」=75+「流速」
で・・・わからないな・・・

「上りの速さ」と「下りの速さ」の比がわかりますよ。
速さの比を求めるためには、「時間の比」と「距離の比」がわかる箇所を探せばいいですね。

はじめの8分で進む距離の比が①と②ですね。

同じ時間に進む距離の比が1:2なら、速さの比は1:2ですね。
つまり、
「上りの速さ」1=75-「流速」
「下りの速さ」2=75+「流速」

そういうことです。
あとは消去算をするだけですね。
消去算は、いろいろなところによくでてきますね。
やり方わかるよね?

はい、□をそろえて消去するやつですよね。
今回は・・・
「上りの速さ」1=75-「流速」
「下りの速さ」2=75+「流速」
□を2にそろえようかな。

それでも解けるけどね。
おススメは「流速」に着目。符号が逆で、数値は同じだよ。
だから、和をとれば消えます。

「上りの速さ」1=75-「流速」
「下りの速さ」2=75+「流速」
和をとると、
3=150
なるほど!つまり、1=50だから、
「上りの速さ」50=75-25
「下りの速さ」100=75+25
つまり、流速は25
求まりました。流速は、分速25mです。

正解です。
今見た通り、流水算で比を活用するのは2パターンあります。
1つ目は、いわゆる「速さと比」の典型的な比の活用。
2つ目は、「上りの速さ」と「下りの速さ」で行う消去算のところ。
どちらか1つの要素だけの問題もあれば、2つの要素が1つの問題の中に入っているものもあるわけです。
ごちゃごちゃにならないように、頭を整理しておいてくださいね。