速さと比
異なる速さで進む2人が、同じ距離を進むとどうなるのか。速さの問題の構成要素として、最重要のものの1つです。
同じ距離を進む
例題
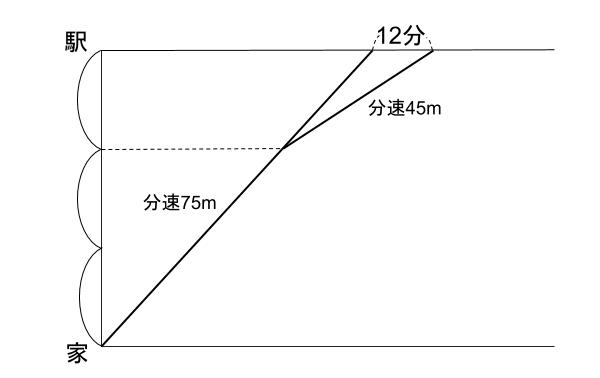
太郎くんは家から駅まで分速75mの速さですすみ、10時30分に駅に着く予定でした。しかし、家から駅までの道のりの \(\displaystyle \frac{2}{3}\) の地点で、速さを分速45mにしたため、駅に着いた時間は10時42分でした。家から駅までの道のりは何mですか。
解説

予定より12分遅れたのは、速さを遅くしたからだね。

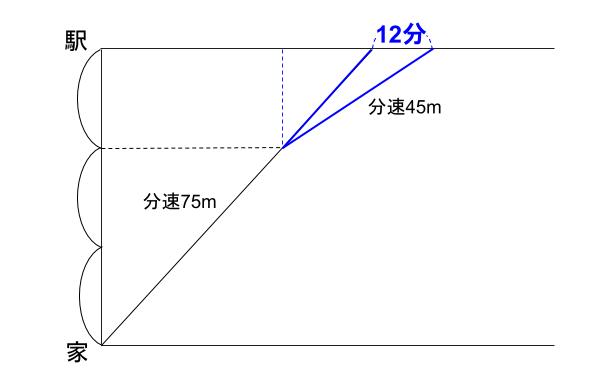
ダイヤグラムにしてみますね。

うん、素晴らしい図だ。この図をみたら、もう次に何に着目するのか、
考える前にわかるようなって欲しい。
「基本の型」があるからね。

「同じ距離」を進む「時間が逆比」パターンですね。
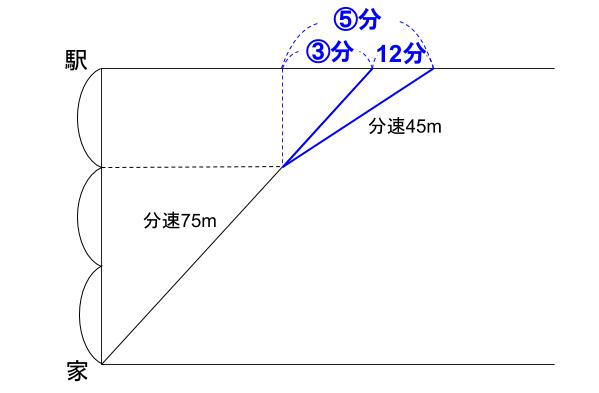
速さの比は75:45=5:3
だから、かかる時間の比は3:5

②=12分だから、③=18分
つまり、家から駅までの道のりの \(\displaystyle \frac{1}{3}\) が求められます。
75×18=1350
45×30=1350
1350mと求まります。
家から駅まではその3倍!
1350×3=4050
求まりました!
4050mです。

大正解!
もちろんこの問題を、線分図で整理して解いてもかまわないよ。