速さと比
異なる速さで進む2人が、同じ距離を進むとどうなるのか。速さの問題の構成要素として、最重要のものの1つです。
同じ距離を進む
例題1
太郎が学校から駅に向かって出発してから20分後に、次郎も学校から駅に向かって出発しました。次郎は出発後30分で太郎を追い越しました。次郎が駅に着いてから4分後に、太郎が駅に着きました。
(1)太郎と次郎の速さの比を求めなさい。
(2)太郎は学校から駅まで何分かかりましたか。
解説

まずは情報整理ですね。線分図かダイヤグラム。

線分図大好きで、ダイヤグラムは食わず嫌いという子が多いのかな。
ダイヤグラムは便利な図だからね。ダイヤグラムを積極的に練習していこうか。

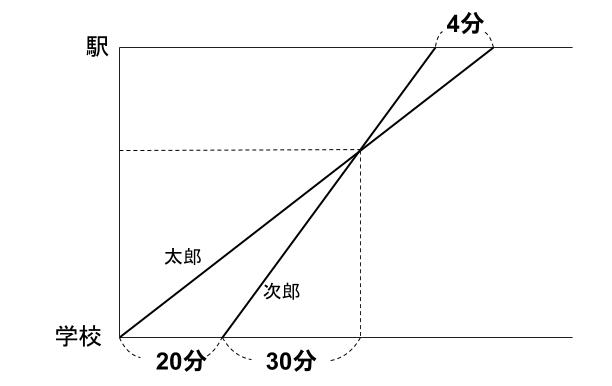
こんな感じですかね。

はい。とてもいいですね。
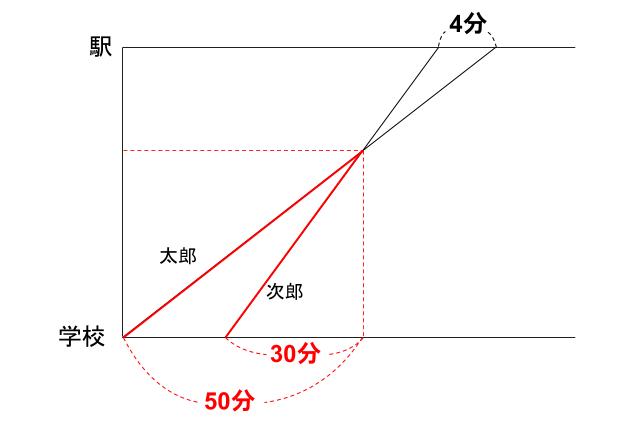
まずは次郎が太郎に追いつくまで。
ここについて考えてみてください。

旅人算の計算はできないから、比ですね。
太郎と次郎を比べる。
速さの比は・・・不明
時間の比は、太郎が50分で次郎が30分
距離の比は・・・あ!
同じ距離を進んでます!
同じ距離タイプです!これは!!

その通りです。
このダイヤグラムも「基本の型」として身につけておきましょうね。
目に焼きつけてくださいな

はい。
で、2人の速さの比は・・・
時間の逆比です。
太郎:3×50分=1
次郎:5×30分=1
太郎と次郎の速さの比は3:5です。

正解!
では続きをやって行こうね!

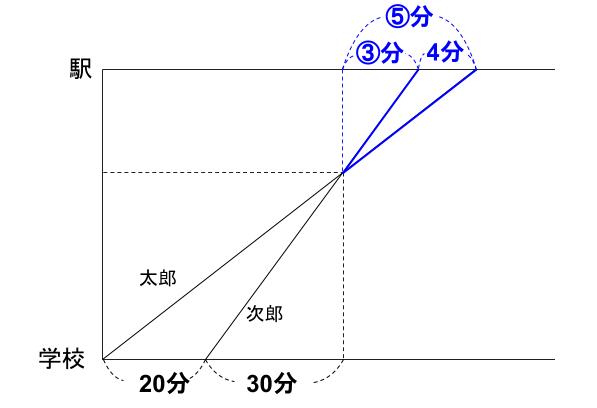
次郎が着いてから4分で太郎が着いたというところ・・・

これも「基本の型」じゃないですか!
2人の速さの比は3:5だから、同じ距離を進むのにかかる時間は逆比の5:3

②=4分だから、⑤=10分
太郎は、50+10=60(分)かかっている。
答えは60分です!

正解です。
同じ地点から進んで、追いつくのも「同じ距離」の代表例。
基本の型として暗記しておきましょうね。