速さと比
同じ距離を進む

1つ前のページで学習した例題1、まだまだこの問題からたくさん学習することが残っています!
例題1・再掲
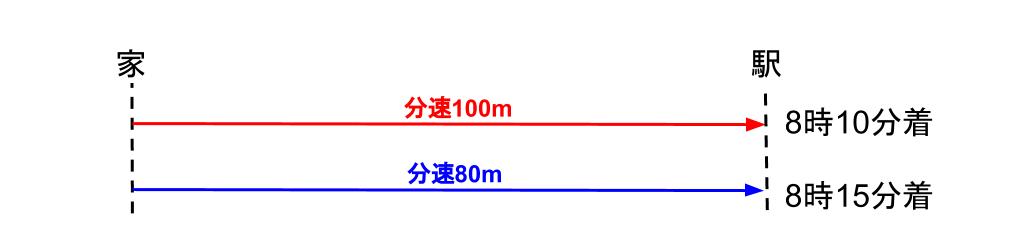
家から駅まで向かいます。分速100mで向かうと8時10分に、分速80mだと8時15分に着きます。家から駅まで何mですか。また、家を出る時刻は何時何分ですか。
解説

ところで、前ページで学習した例題1だけど、線分図はあまり役に立たなかったでしょ。

はい、書いてみたけれどうまく使えませんでした・・・
こんな図を書いたのですけど。

この図はね、「図をかいたことによって何かがわかる!」という図ではないんだよ。
この図から何か答えを導き出すことはできないんだ。
この図は、「2人が同じ距離を進んだ」から「時間は逆比だ」って思い出してもらうための図。

?どういうことですか?

つまりね、「異なる速さの2人が同じ距離を進むとき、かかる時間は速さの逆比」という事実は、「暗記」してしまえということです。
これは、線分図から導かれることではなくて、式から導かれることだからね、線分図をかいて、それをじっと見ていてもでてくることじゃないのです。
だから、「暗記」です。
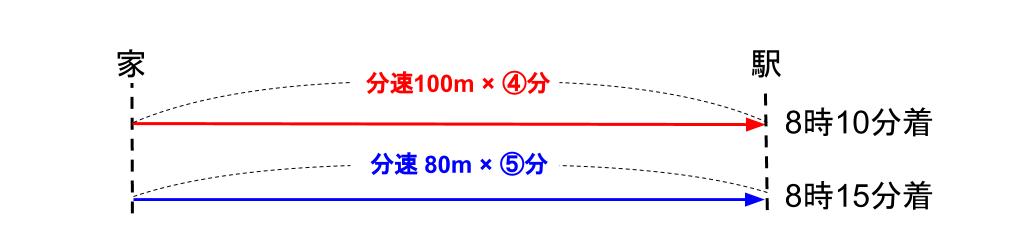
「暗記した事実=時間が逆比」も、図に同時に書きこめるようなってください。
下のように、④分と⑤分ね。

図を見て、同じ距離進んでる!
と気づいたら、「時間が逆比」はすぐに思い出せるようにしておくのですね。
考えて導くのではなくて。

その通り。
図をかくまでもなく、問題文を読んだ時点で
「同じ距離進んでるから時間が逆比だ」って思い出せれば、線分図は必ずしも書く必要はないよ。
式処理だけで答えを出してもいい。
「同じ距離進んでるから時間が逆比」は「速さの基本の型」にすぎません。考え込んで求めることではないのです。
九九みたいなものです。
今後、より複雑な問題を構成するための部品にすぎないのです。
しっかりと「完璧な理解と暗記」をしてください。

はい。
線分図についてさらに研究

さて、今まで旅人算を線分図で表現してきたとき、必ず「同じ時間」での動きを表現してきたよね。
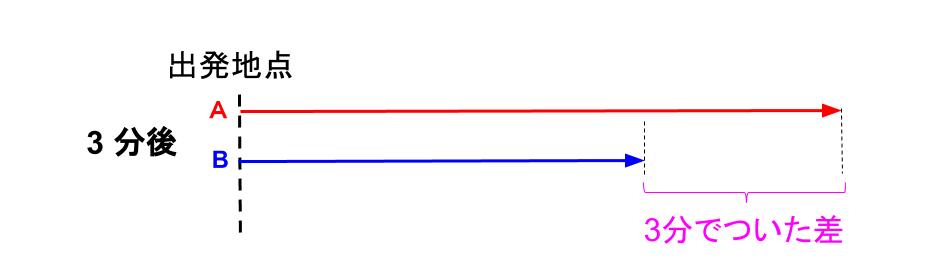
例えば、AくんとBくんの2人が、同時に同じ方向に出発して、出発から3分後の図は下図のようにかいてきたね。

速さを線分図で表すとき、「同じ時間での動きをかく」というのは、絶対のルールではないけれど、とても表現しやすい表し方なのは間違いない。
だから、今後もこのように線分図を使っていくことにしよう。
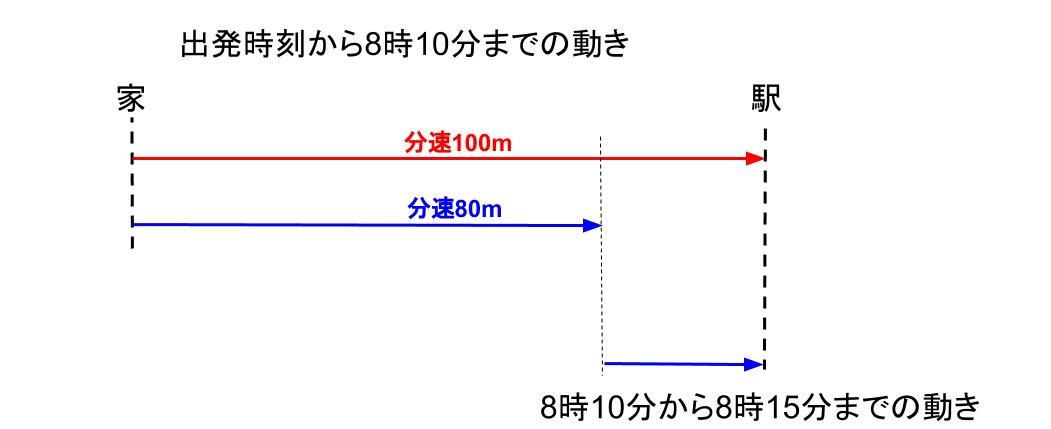
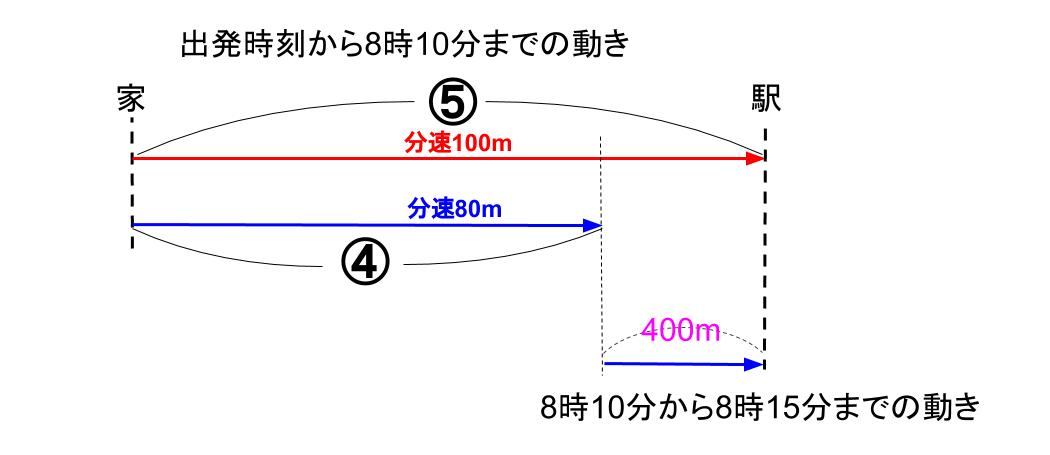
今回の例題を、式処理ではなく線分図をフル活用して解くのならば、下図のように2段階の図にします。
「同じ時間での動きをかく」を意識して書いた線分図です。

この図に、わかる情報を書きこめば、この問題は解けますよ。
ヒントは、「同じ時間」に着目してるということ。

「異なる速さの2人が、同じ時間を進む」のですね。
「速さの比」と「進んだ距離の比」が一致します。
速さの比が、100:80=5:4なので、
進んだ距離の比も5:4です。

距離の差①は、分速80mで5分進んだ距離、400mだ!
家から駅までの距離は、⑤=2000m
確かに解けました!

うん。算数において、「必ずこうやって解かないといけない」という決まりはない。
だから、何に着目するのかで、図も変わってくる。
様々な方向から考えて、様々な解き方を見つけていくことが実力アップには大事なんだ。
でもね、この問題は「異なる速さの2人が、同じ距離を進む問題」として解けるようになって欲しい。さっきも言ったのだけど、基本の型だからね。
ややこしく解かないで、スパッと逆比で解いてほしい。

そういうものなんですね。
わかりました。
大多数の生徒は、まずは「基本の型」にはまることを大事にしましょう。