速さ・比の活用
「速さと比」は、多くの生徒が不得意とする単元です。しかし、中学受験においては主役の単元であり、この単元での得点力は、合否に直結すると言っても過言ではないでしょう。
速さの比の基礎の基礎
例題1
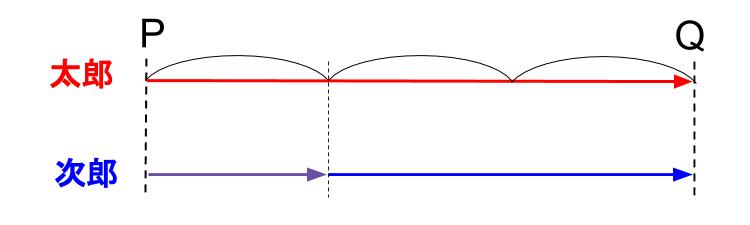
P地点からQ地点までの道のりを太郎と次郎が歩きました。太郎はずっと時速5kmで歩きました。次郎は全道のりの \(\displaystyle \frac{1}{3}\) を時速4kmで、残りを時速6kmで歩きました。2人のかかった時間の比を求めなさい。
解説

けっこう複雑ですね・・・

まだまだ序の口だよ。
ちょっと整理してみたら、すぐに解決するよ。
やってごらん。

速さを変える前と後で、次郎(前)、次郎(後)とします。
太郎と次郎(前)と次郎(後)の進んだ距離の比がわかります。
3:1:2ですね。
速さは問題文で与えらているので、
(速さ)×(時間)=(距離)
太郎 :5×?=3
次郎前:4×?=1
次郎後:6×?=2
となります。
なるほど、あとは計算するだけですね!
時間の比は計算するだけです。

その通り!あとは計算するだけです。
ところで、今回は比を求めるのだから、P地点からQ地点まで間の道のりは3でなくてもいいよね。
30でも300でも、どんな値でも構わない。
うまい数値を選べば、計算が整数だけで済むからね。

なるほど、じゃあえっと・・・60倍してみます。5でも4でも6でも割れるようになるから。P地点からQ地点まで間の道のりは180とします。
(速さ)×(時間)=(距離)
太郎 :5×?=180
次郎前:4×?=60
次郎後:6×?=120
順に時間を計算すると、
(速さ)×(時間)=(距離)
太郎 :5×36=180
次郎前:4×15=60
次郎後:6×20=120
太郎は36、次郎は、15+20 =35
かかった
時間の比は、36:35です!

大正解だね!