速さと比
速さの比の基礎の基礎

いよいよ速さに比の要素を導入します。これで最終形です。
まずは、今まで学んだことをおさらいしておきます。
(速さ)×(時間)=(距離)
これだけです。「速さ」の問題を成り立たせる仕組みは、この式たった1つです。この1つだけで、今までの速さの問題は作られていました。

え・・・?「通過算」とか「流水算」とかいろいろあったけど。
たった1つの式でしたっけ?

はい、たった1つです。
「通過算」も「流水算」も、「速さの基本的な仕組み」に「おまけの要素」があっただけです。
根幹となる仕組みは、
(速さ)×(時間)=(距離)
これだけでしたよ。
次に「通過算」や「流水算」を学習するときは、これを意識して解いてみてね。

で、旅人算は、「速さ」と「距離」が、少しだけアレンジされているだけ。
(AとBの速さの和)×(時間)=(AとBの距離の和)
(AとBの速さの差)×(時間)=(AとBの距離の差)
2人の和、差に変わっただけです。
(速さ)×(時間)=(距離)
というたった1つの式です。

そう言われてみれば、そうなのかな・・・

そうですよ。
そして、この速さの「3つの要素」である「速さ・時間・距離」のうち、2つが問題で与えられます。これを用いて最後の1つを計算するだけです。
今までやってきた問題は突き詰めればこれだけなのです!

そして「速さと比」も、これと大差はありません。
「比」というくらいですから、2人の進み方を比べるわけですが、特に難しいことはありません。例題で見ていこうね!
例題1
太郎の歩く速さは分速45m、次郎の歩く速さは分速75mです。2人は健康のために毎朝散歩をします。ある日、太郎は20分、次郎は10分散歩をしました。この日の2人の歩いた距離の比を求めなさい。
解説

ただの計算問題じゃないですか。

そうですよ。
きちんと計算しましょう。
(速さ)×(時間)=(距離)
とにかく、この式1つにつきることを理解して下さいね。

(速さ)×(時間)=(距離)
太郎:45×20=900
次郎:75×10=750
2人の進んだ距離の比は、900:750=6:5
求まりました。
6:5です。

うん。正解。
難しく考える必要はないよ。

さて、ここで確認しておきたいことがある。
それは、
(速さの比)×(時間の比)=(距離の比)
ということなんだ。
※厳密にはこのような表記はしませんが。
太郎と次郎の速さの比は、
45:75=3:5
太郎と次郎の進んだ時間の比は、
20:10=2:1
これらの比を用いて、太郎と次郎の進んだ距離の比は計算できます。
太郎:3×2=6
次郎:5×1=5
2人の進んだ距離の比は6:5
さっき、具体値で求めたものと一致しますね!

はい。
そうですね。
具体値でなく、比で計算しても求まりますね。

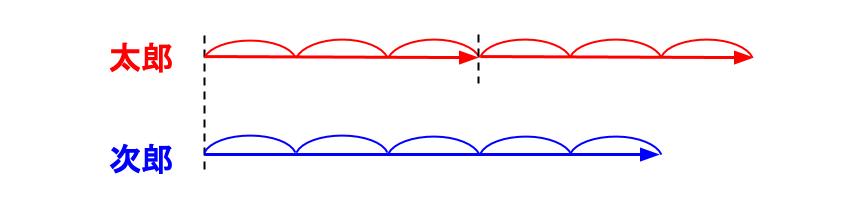
結局は、下図のようになっているということなんだ。
1山の具体値は関係ないのです。

10分で太郎は3山、次郎は5山進む。
太郎は20分で、6山進む。
1山が何mであってもこれが成り立つということか!