正六角形の内部の点
例題9
図のように、正六角形ABCDEFの内側に点Pをとり、6つの頂点とPをそれぞれ直線で結びます。三角形ABP、CDP、EFPの面積が3 \(cm^2\)、5 \(cm^2\)、8 \(cm^2\)であるとき、三角形BCPの面積を求めなさい。
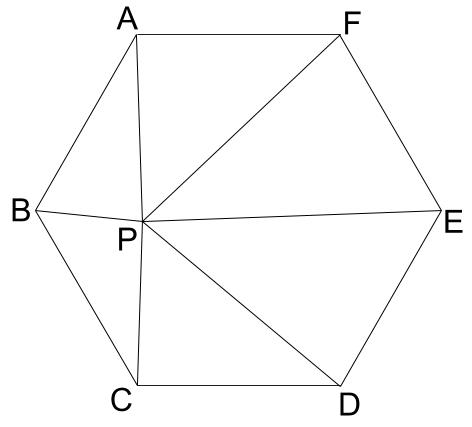
解説

難問です。灘中学校での出題です。
今までの知識とどのように結びつけるか、これこそが算数の難問に対するアプローチです。

2つの解法を示します。
まずは正六角形に対する定番のアプローチです。
正六角形を6等分した正三角形、これを用います。
次の図のように、正六角形の外側に並べます。
底辺も高さも等しい三角形が3つ並ぶことがわかります。
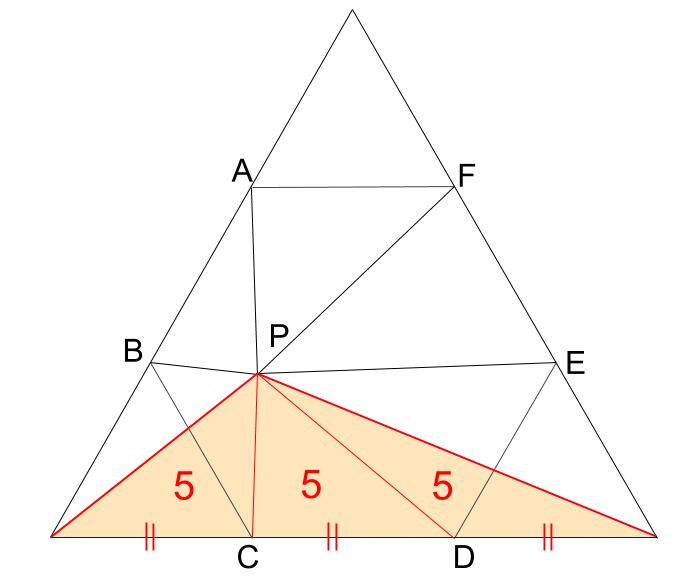

同様に、他の方向にも面積の等しい三角形が並びます。
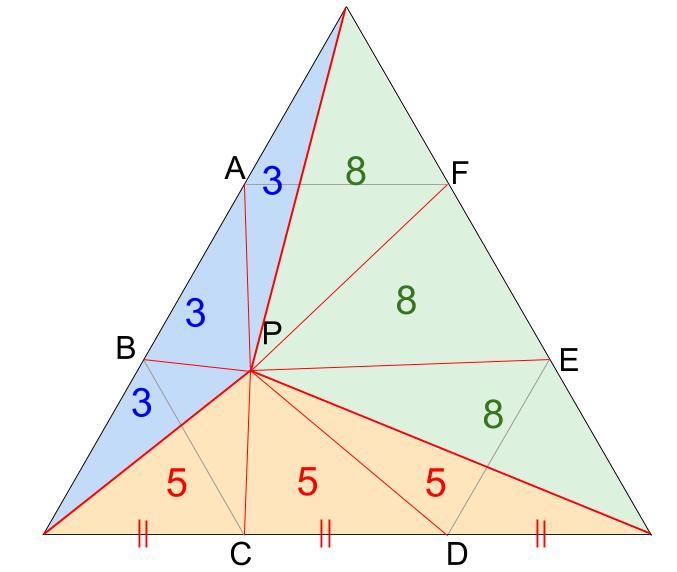

大きな正三角形全体の面積は、48 \(cm^2\) です。
正六角形ABCDEFは、
48×\(\displaystyle \frac{6}{9}\)=32 (\(cm^2\))です。
また、次の図の向かいあう2つの三角形の面積の和は等しいです。
高さの合計が等しいからです。
その面積は、正六角形ABCDEFを6等分したうちの2つ分だから、
32×\(\displaystyle \frac{2}{6}\)=\(\displaystyle \frac{32}{3}\) (\(cm^2\))です。
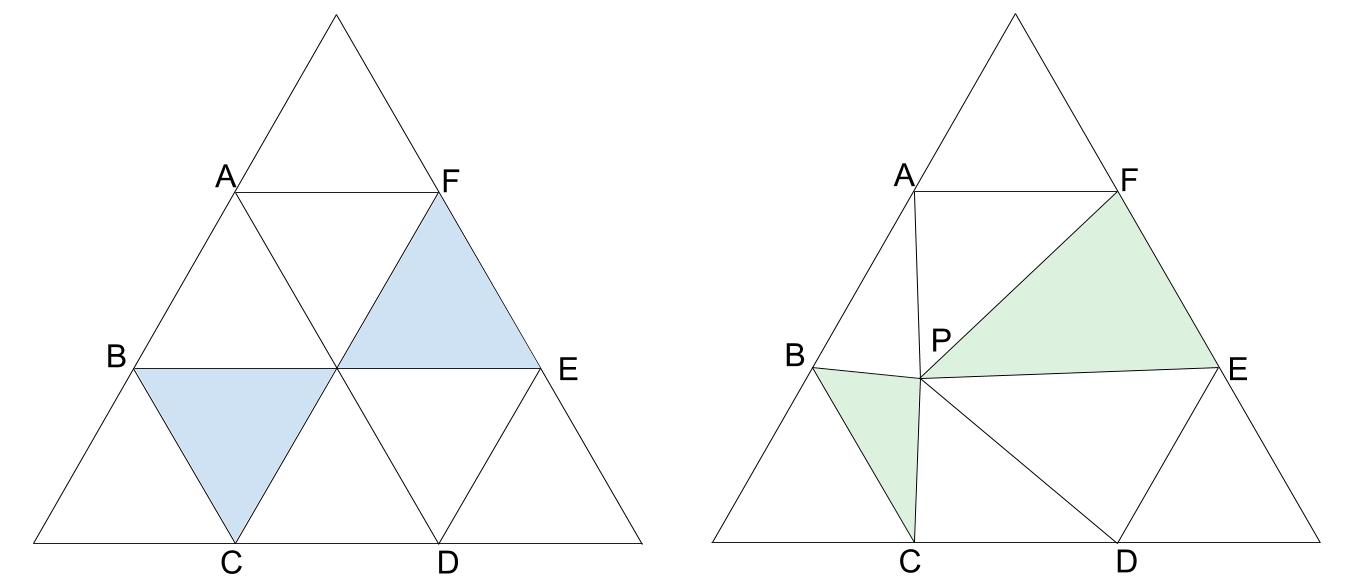

よって、三角形BCPの面積は
\(\displaystyle \frac{32}{3}\)-8= \(\displaystyle \frac{8}{3}\) (\(cm^2\))
別解

「正三角形の内部の点Pから、それぞれの辺に引いた垂線の長さの和が一定」
この知識を使って解くこともできます。
※くわしくは、「正三角形」で扱っています。
三角形ABP、CDP、EFPの面積の和は、点Pがどこにあっても一定です。
その和は、3+5+8=16 (\(cm^2\))です。
これを3等分すると、\(\displaystyle \frac{16}{3}\) \(cm^2\) ずつになります。
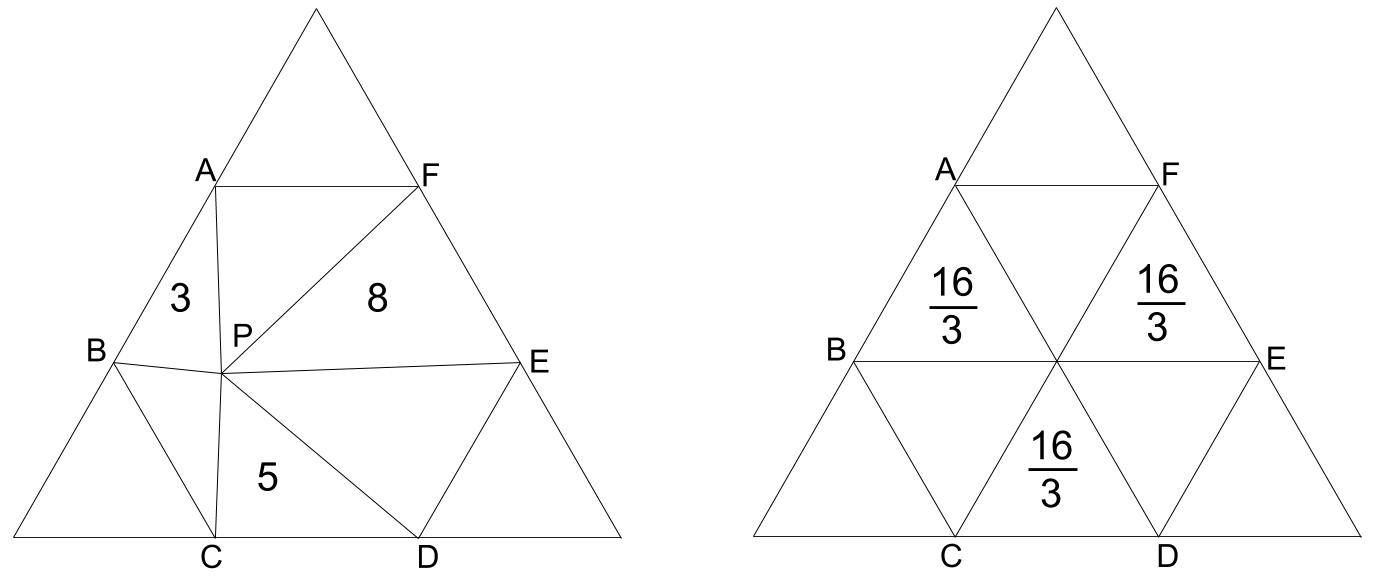

このことから、もとの正六角形の面積が32 \(cm^2\)であることがわかります。
この続きは、はじめの解き方と同じです。
