相似の利用
例題8
下の図の正六角形ABCDEFで、点Mは辺BCの真ん中の点、点Nは辺EFの真ん中の点、点Pは辺AFの上にあります。このとき、次の各問いに答えなさい。
(1)Pが辺AFの真ん中の点となるとき、三角形PMNの面積は正六角形ABCDEFの面積の何倍ですか。
(2)MPとPNの長さの和が最も小さくなるとき、AP:PFを求めなさい。
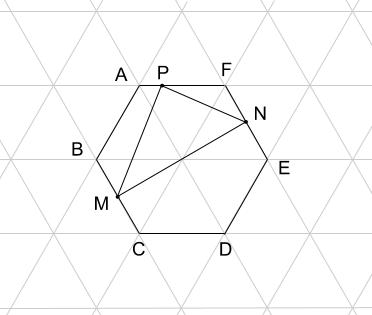
解説
(1)Pが辺AFの真ん中のときの三角形PMNの面積

三角形PMNですが、どこを底辺としてどこを高さと見るのが解き易そうでしょうか?
点Pは動く点ですから、MNを底辺とするのが解きやすいですね。
ですから、三角形PMNと面積を比較する相手は、三角形ABFや三角形ACEがよさそうです。
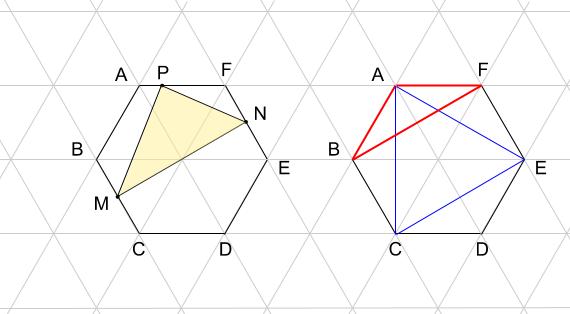

では三角形ABFと比較することにしましょう。
点PがAFのまんなかの点のときです。
三角形PMNと三角形ABFを比較します。
底辺は1:1
高さは1.5倍です。
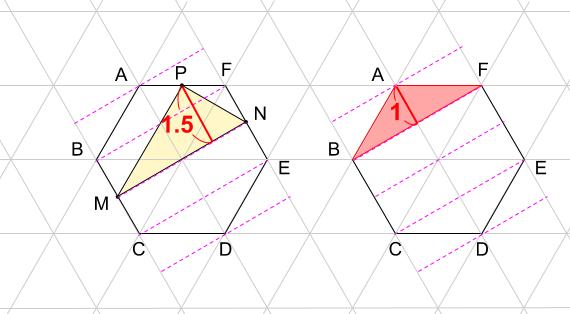

三角形ABFの面積を1とすると、三角形PMNの面積は1.5、また、正六角形ABCDEFの面積は6です。
より、三角形PMNの面積は正六角形ABCDEFの面積の、\(\displaystyle \frac{1.5}{6}\)=\(\displaystyle \frac{1}{4}\) です。
(2)MPとPNの長さの和が最も小さくなるときのAP:PF

完全に知識です。
MPとPNですが、鏡AFで反射したようになるときに、その和が最小になります。
つまり、AFが鏡ならば、点Nは鏡の中のどこに見えるかを作図します。
その位置をN´とします。
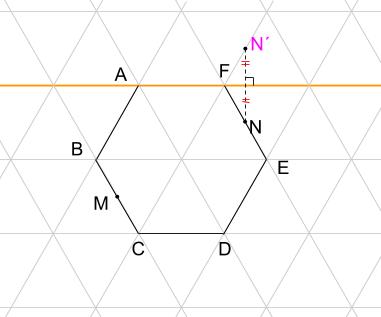

MとN´を結びます。
AFとの交点が求めるPの位置です。
Pがこの位置にあるときに、MP+PNが最小になります。
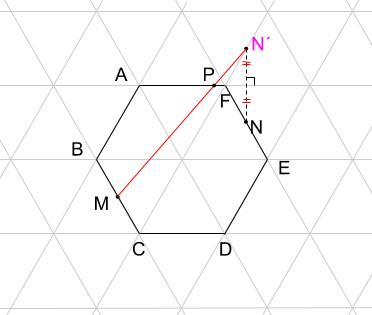

ここまでくれば、あとは普通の平面図形の問題です。
AP:PFはどうすれば求められるのか・・・
平行線がたくさんありますし、相似の定番である砂時計かピラミッドにもちこみましょう。
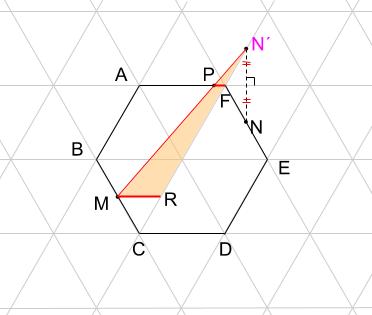

三角形N´PFと三角形N´MRがピラミッド型相似になっています。
相似比は、高さからわかりますね。
三角形N´PFの高さは、小正三角形の高さの半分
三角形N´MRの高さは、小正三角形の高さの2倍
つまり、相似比は、0.5:2=1:4です。
よって、PFの長さは、MRの長さの \(\displaystyle \frac{1}{4}\) です。
MRの長さは正三角形の1辺の長さの \(\displaystyle \frac{1}{2}\) なので、
PF=AF×\(\displaystyle \frac{1}{2}\)×\(\displaystyle \frac{1}{4}\)
つまり、PFはAFの\(\displaystyle \frac{1}{8}\)
よって、AP:PF=7:1
と求まります。
