相似の利用
- 例題7
-
下の図は、それぞれ同じ大きさの正六角形をすき間なくかいたものです。点A、Bは正六角形の頂点で、点P、Qは、AとBを結ぶまっすぐな線と正六角形の辺との交わった点です。ABの長さが30cmのとき、APとPQの長さをそれぞれ求めなさい。
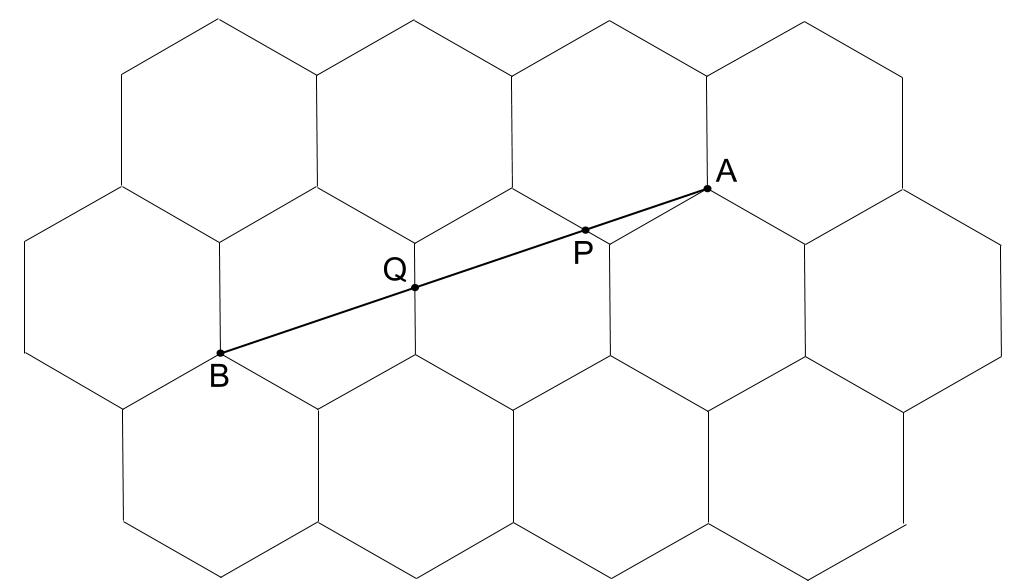
- 解説
-

正六角形が平面にしきつめられています。
ハチの巣みたいですね。
正六角形はもちろん正三角形に分割できます。
また、平行線がたくさんあるので、
砂時計型相似、ピラミッド型相似を利用できるように補助線を引くことを考えます。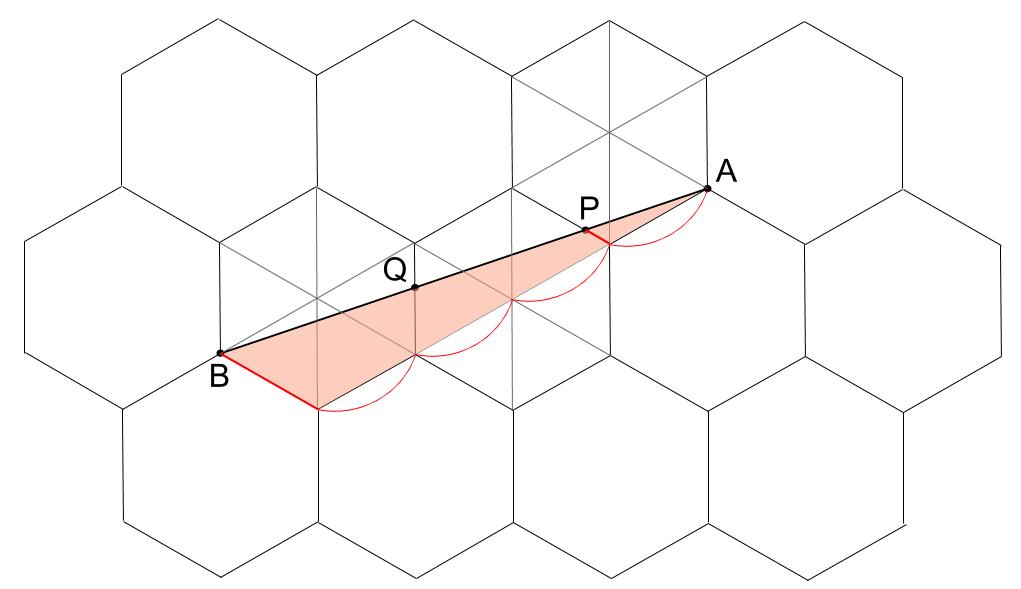

上図のピラミッド型相似より、
APはABの長さの \(\displaystyle \frac{1}{4}\) ですね。
AB=30cmなので
AP=7.5cm
4:1ですね。
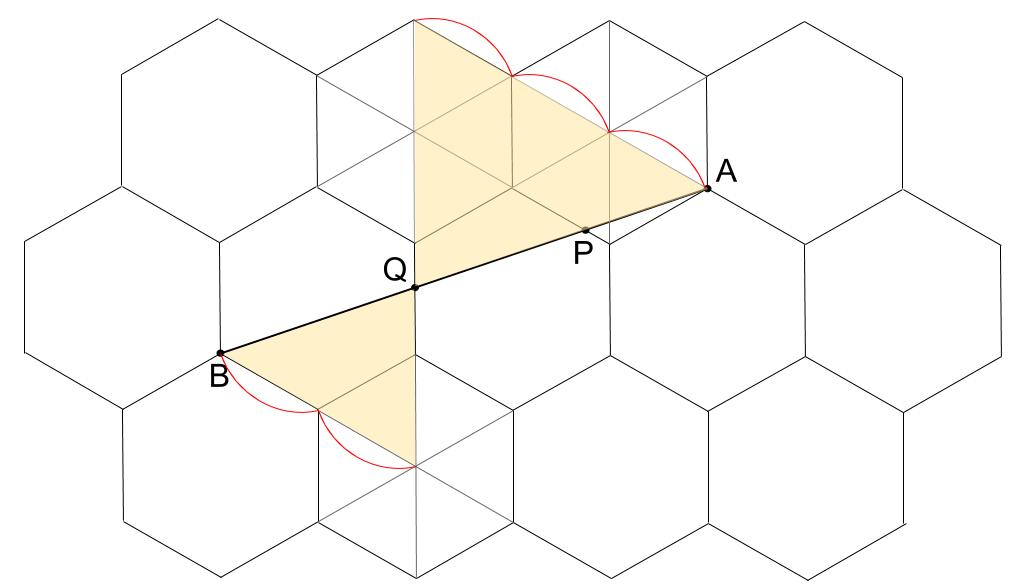

上図の砂時計相似の相似比が3:2なので、AQとQBの長さの比も3:2
つまり、AQの長さはABの長さの\(\displaystyle \frac{3}{5}\) なので、
AQ=30× \(\displaystyle \frac{3}{5}\) =18cm
となります。
よって、PQ=18−7.5=10.5(cm)
となります。
筑波大学附属駒場中学校での出題からでした。
