正六角形に関する重要知識・その６

基本６分割と延長

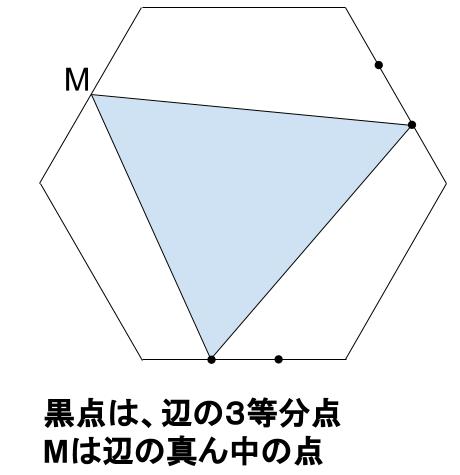
解説

水色の部分に着目しても解けません。

白い部分に着目します。
すると、以前に学習した問題と同じように解けます。

外側に延長するのです。

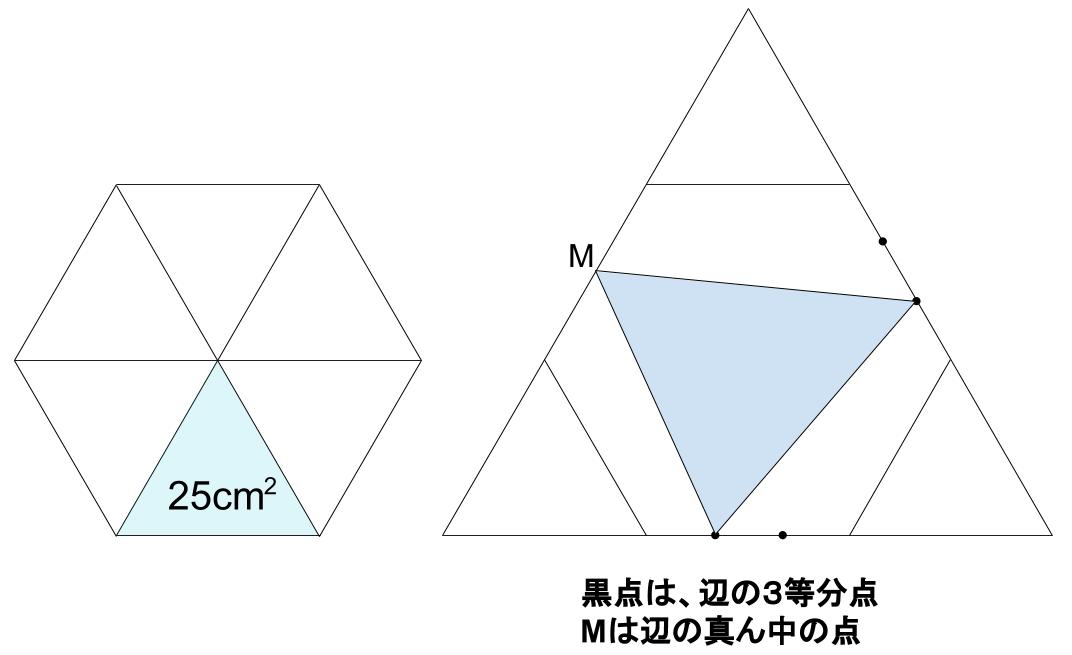
大きい正三角形ができました。
そこから、３つの角を切り落としていけば、水色部分が残るわけです。

大きい正三角形の面積は・・・

小正三角形が９つ分なので、
25×９＝225（\(cm^2\)）
ですね。

はい、225 \(cm^2\) です。

では、３つの角です。

まずは、左下からいきますね。

小正三角形と比べて、底辺が \(\displaystyle \frac{4}{3}\) 倍。
高さは \(\displaystyle \frac{3}{2}\) 倍です。

よって、25× \(\displaystyle \frac{4}{3}\)× \(\displaystyle \frac{3}{2}\)=50（\(cm^2\)）

前にもやりましたね。大丈夫かな？

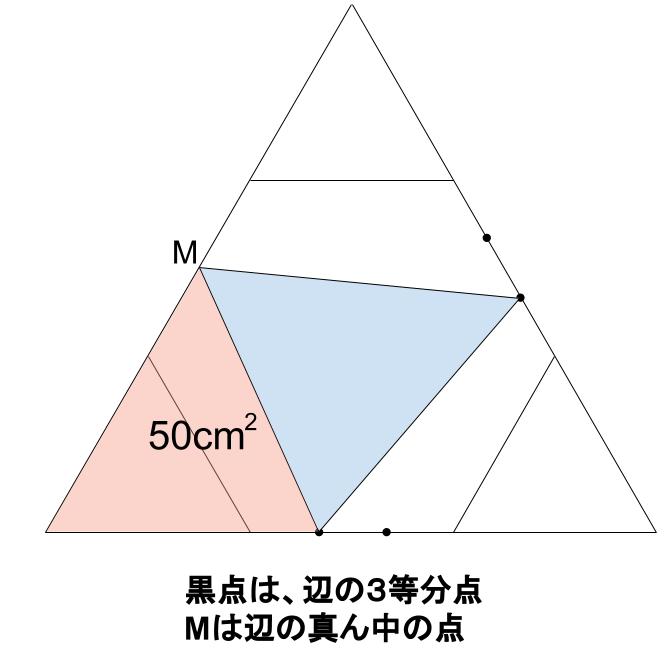
はい、わかります。

右下は、
小正三角形と比べて、底辺が \(\displaystyle \frac{5}{3}\) 倍。
高さは \(\displaystyle \frac{4}{3}\) 倍です。

よって、25× \(\displaystyle \frac{5}{3}\)× \(\displaystyle \frac{4}{3}\)= \(\displaystyle \frac{500}{9}\)（\(cm^2\)）

上は、
小正三角形と比べて、底辺が \(\displaystyle \frac{5}{3}\) 倍。
高さは \(\displaystyle \frac{3}{2}\) 倍です。

よって、25× \(\displaystyle \frac{5}{3}\)× \(\displaystyle \frac{3}{2}\)= \(\displaystyle \frac{125}{2}\)（\(cm^2\)）

はい、その通りです。

大正三角形から、角の３つを引けば水色部分になるから、

225－（50＋\(\displaystyle \frac{500}{9}\)＋ \(\displaystyle \frac{125}{2}\)）＝\(56\displaystyle \frac{17}{18}\)（\(cm^2\)）

正解です。

別解

もともとの正六角形の１辺を、２等分か３等分しているので、１辺の長さを６とおけば、分数がでてきません。

上と同じ解き方だけどね。
途中の計算で分数がでてこなくなります。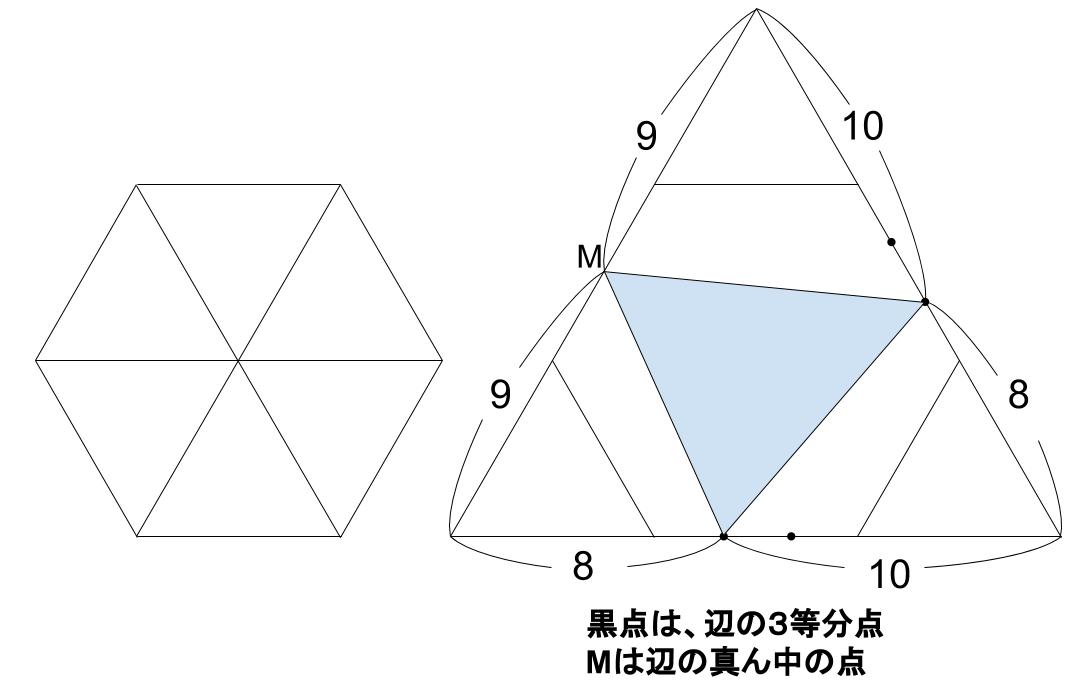

１辺の長さが１の正三角形の面積を１とします。
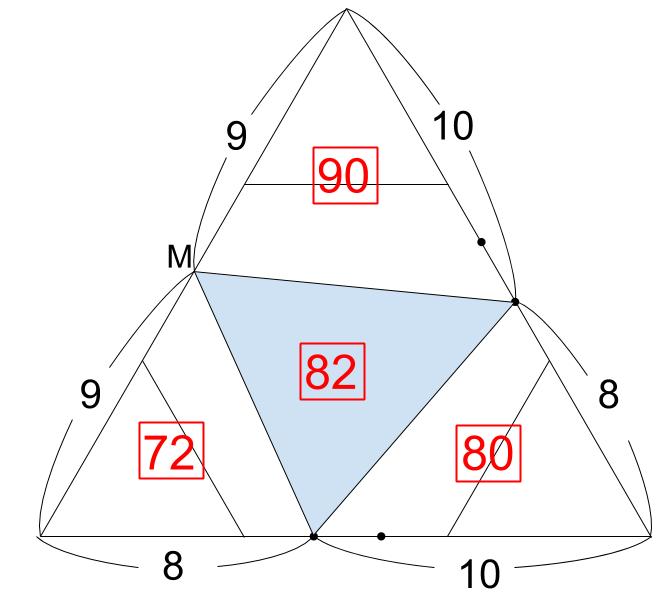
面積 25\(cm^2\) の小正三角形の面積は、６×６＝36より36となります。

大正三角形の面積は、18×18＝324より324
左下は、８×９＝72より72
右下は、10×８＝80より80
上は、10×９＝90より90
水色部分は、324－（72＋80＋90）＝82

25×\(\displaystyle \frac{82}{36}\) ＝\(56\displaystyle \frac{17}{18}\)（\(cm^2\)）