基本6分割と延長
- 例題5−1
-
次の図において、外側の図形は正六角形で、面積が150 \(cm^2\) とします。
正六角形の内部にある水色部分の面積を求めなさい。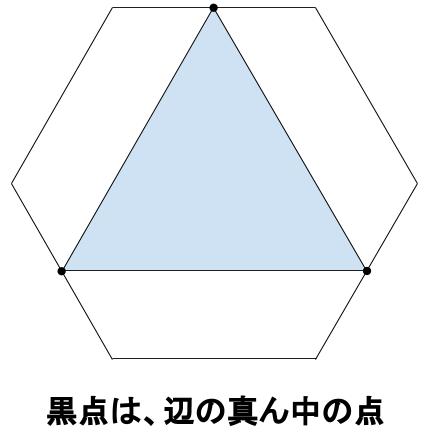
- 解説
-

大事な解法を2つ示します。
外部に延長

いつもの6分割をして、小正三角形に分けたあと、
さらにその正三角形を、正六角形の外部につけ足します。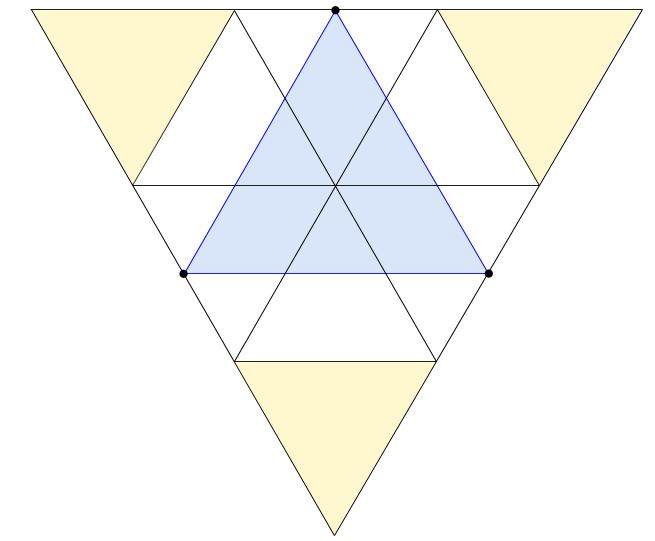

新しくできた、下向きの大正三角形の面積から、水色部分の面積が求められます。


下向きの大正三角形の面積は、25 \(cm^2\) が9個分
水色部分は、下向きの大正三角形を4等分しています。
つまり、
25×9×\(\displaystyle \frac{1}{4}\)=56.25(\(cm^2\))
なるほど。求まりました。

はい、その通りですね。正解です。
外部への延長もとてもよく使いますからね。覚えておきましょう。
別解・内部を分割

今回は、すべて辺のまん中の点なので、
正三角形を均等に分割する解法も楽そうです。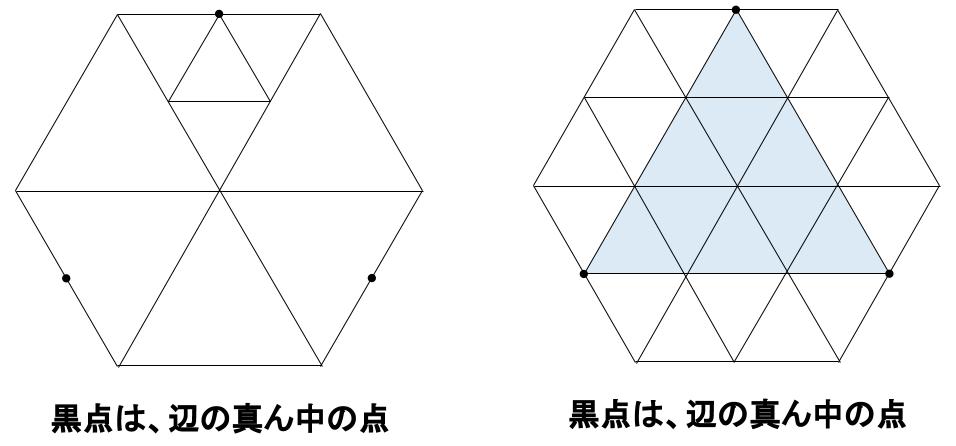

正三角形を、さらに小さい正三角形4つに分割ですね。
6個の正三角形すべてを分割すれば、
6×4=24全体の正六角形が24等分されました。
水色部分は、そのうち9個分なので、
150× \(\displaystyle \frac{9}{24}\)= \(\displaystyle \frac{225}{4}\)=56.25(\(cm^2\))
求まりました。

はい、正解です。
- 例題5−2
-
下図において、外側の図形は正六角形で、面積が150 \(cm^2\) です。
正六角形の内部にある水色部分の面積を求めなさい。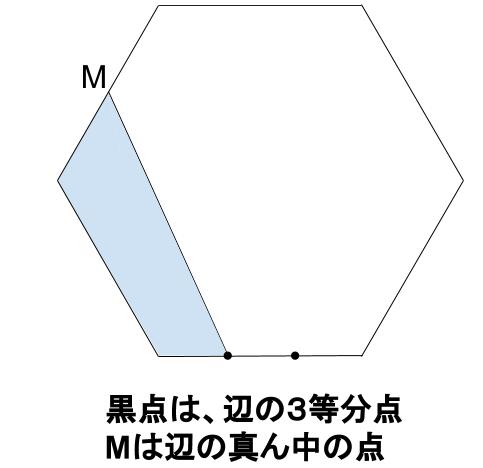
- 解説
-

はじめてだとなかなか難しい問題です。
まずは、いつもの6分割です。
正六角形を、正三角形6つにわけます。
正三角形1つの面積は、150÷6=25 \(cm^2\) です。そして、次の図のように、左下に延長します。
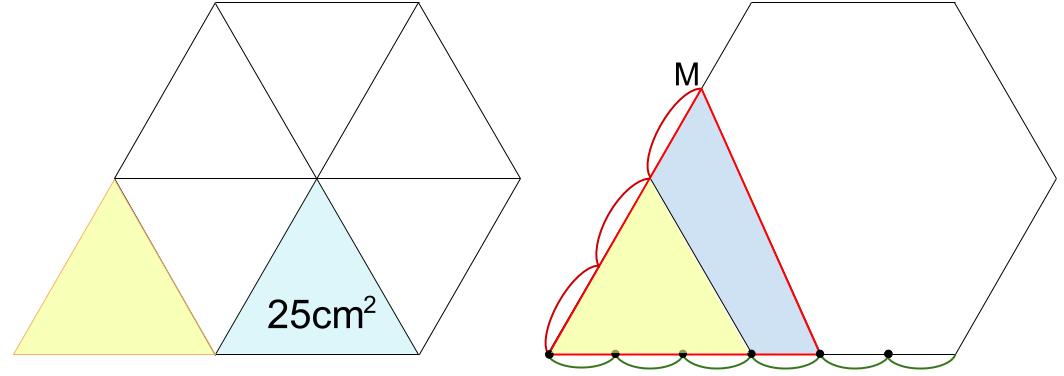

上図の赤い三角形は、
面積が 25 \(cm^2\) の小正三角形と比べて、底辺が \(\displaystyle \frac{4}{3}\) 倍。
高さは \(\displaystyle \frac{3}{2}\) 倍です。よって、25× \(\displaystyle \frac{4}{3}\)× \(\displaystyle \frac{3}{2}\)=50(\(cm^2\))
水色部分の面積は、黄色い正三角形の面積を引いて、
50−25=25(\(cm^2\))これで求まりました。

なるほどー

延長なしで、内部の分割だけでも解けます。
