正六角形に関する重要知識・その３

正六角形の基本６分割

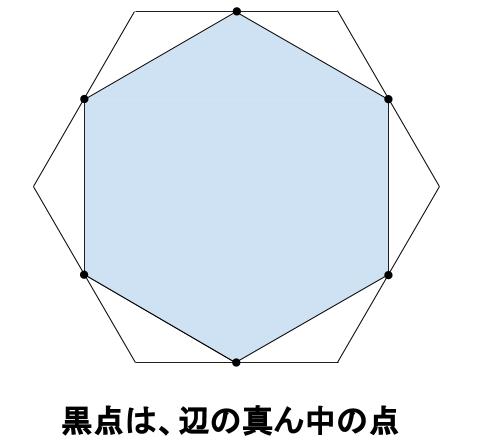
解説

水色の六角形は正六角形ですよね。

はい、そうです。感覚的にわかるよね。

で、問題を解くときは、内部の正六角形ではなく、
まわりの三角形に着目します。
すると、今までと同じ解き方で解決します。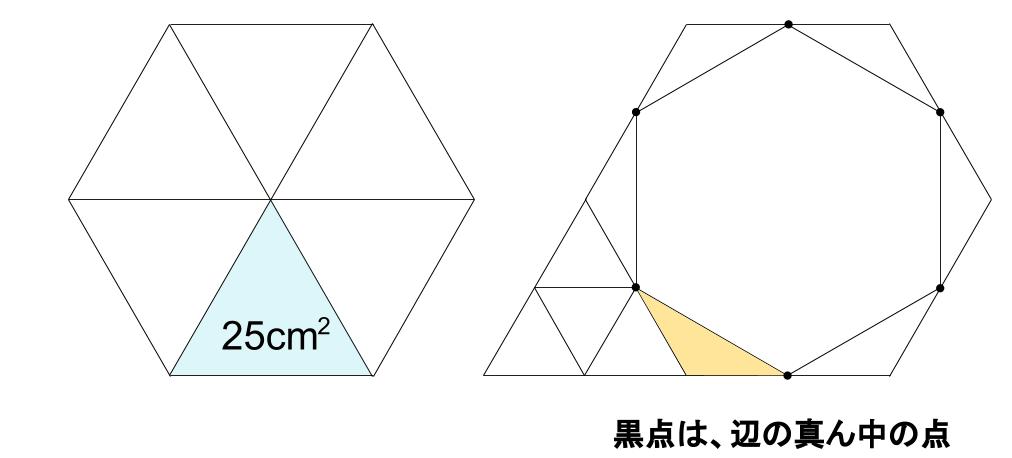

正六角形を、６つの小正三角形に割ります。
小正三角形の面積は、150÷６＝25 (\(cm^2\))

上図の黄色い三角形は、小正三角形と比べて、底辺が \(\displaystyle \frac{1}{2}\) 倍。
高さも \(\displaystyle \frac{1}{2}\) 倍です。

よって、25× \(\displaystyle \frac{1}{2}\)× \(\displaystyle \frac{1}{2}\)= \(\displaystyle \frac{25}{4}\) (\(cm^2\))

求める面積は、全体からこの三角形６つを引いたものだから、

150ー \(\displaystyle \frac{25}{4}\)×6＝112.5 (\(cm^2\))

はい、正解です。

別解

別解として、内側の正六角形を、いつもの６分割します。

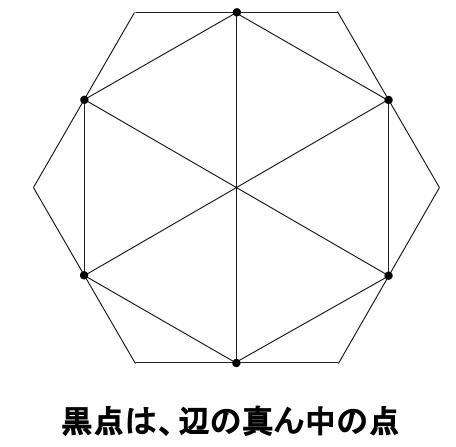
それぞれ小正三角形の重心をとって、三角形に分割します。

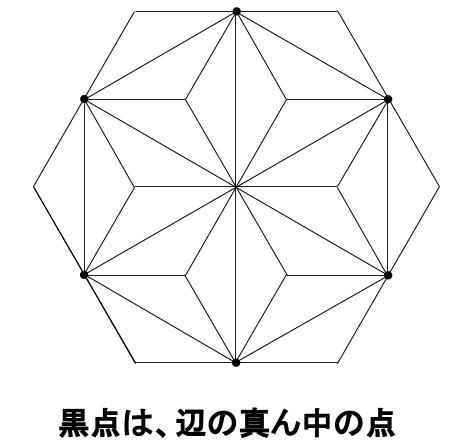
図形全体が、24等分されます。

とてもきれいな分割ですが、この分割はめったにでてこない分割です。
はじめに紹介した解法を身につけておきましょう。

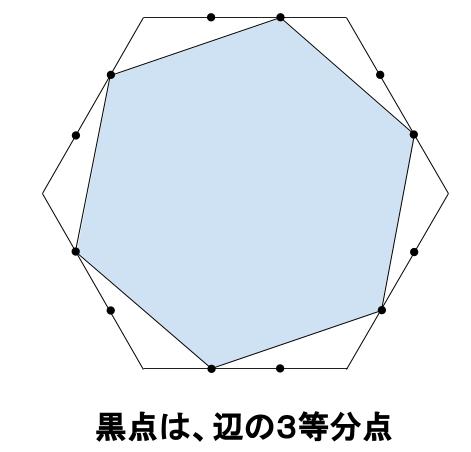
解説

先と同じ解き方をするだけですね。

注目するのは、水色の六角形ではなくて、まわりの三角形です。

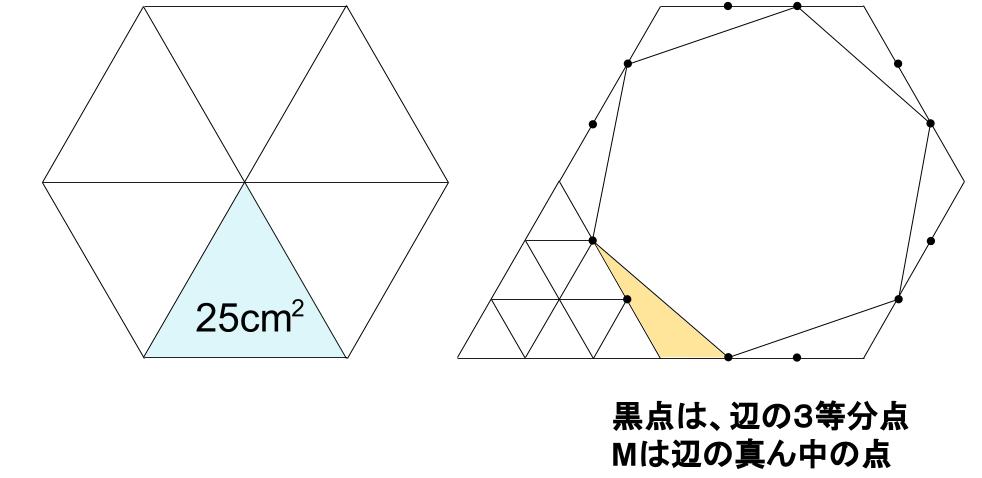
正六角形を、６つの小正三角形に割ります。
小正三角形の面積は、150÷６＝25 (\(cm^2\))

小正三角形と比べて、底辺が \(\displaystyle \frac{1}{3}\) 倍。
高さは \(\displaystyle \frac{2}{3}\) 倍です。

よって、25× \(\displaystyle \frac{1}{3}\)× \(\displaystyle \frac{2}{3}\)= \(\displaystyle \frac{50}{9}\) (\(cm^2\))

求める面積は、全体からこの三角形６つを引いたものだから、

150ー \(\displaystyle \frac{50}{9}\)×6＝\(\displaystyle \frac{350}{3}\)＝\(116\displaystyle \frac{2}{3}\) (\(cm^2\))
求まりました。

正解です。
内側の正六角形を分割しても、決して解きやすくはなりません。