正六角形の基本6分割
- 例題1
-
次の各図において、外側の図形は正六角形で、面積が150 \(cm^2\) とします。
それぞれの図について、正六角形の内部にある水色部分の面積を求めなさい。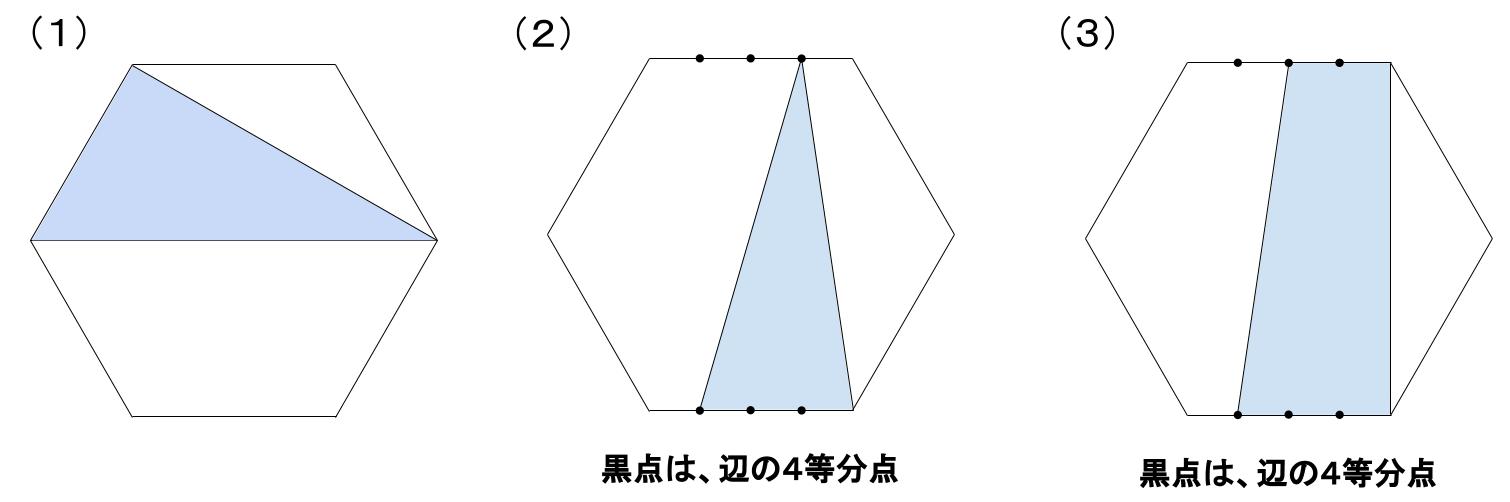
- 解説
-

正六角形と三角形の面積の比較です。
もちろん正六角形を、6つの小正三角形に割ります。
これこそが正六角形に関する最重要知識です。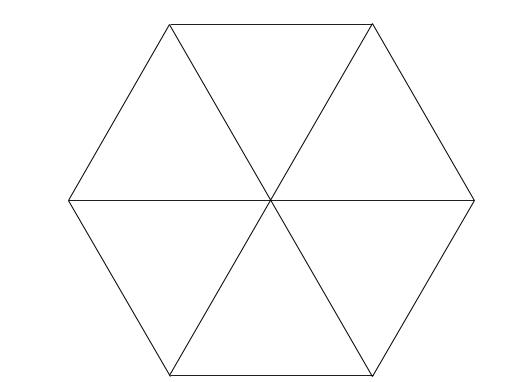

この小正三角形と求める三角形の
「底辺の比」
「高さの比」
をそれぞれ求めます。
そこから面積比を求めることができます。(1)
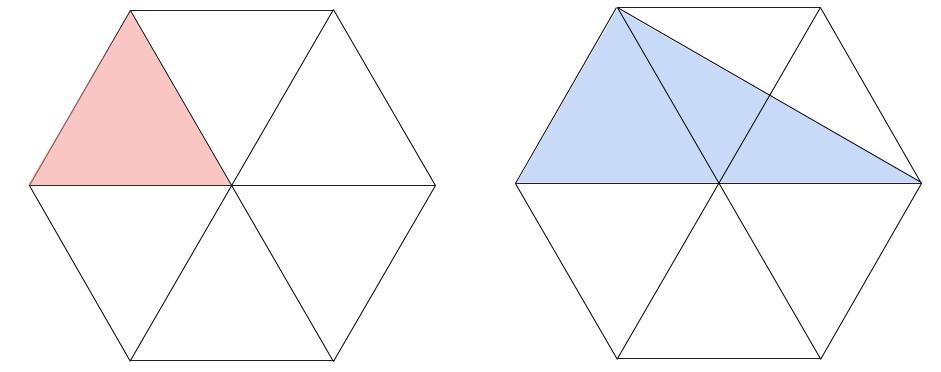

小正三角形の面積は、150÷6=25(\(cm^2\))
小正三角形と比べて、底辺が2倍。
高さは1倍です。よって、25×2×1=50 (\(cm^2\))
求まりました。50 \(cm^2\) です。

正解です。
(2)
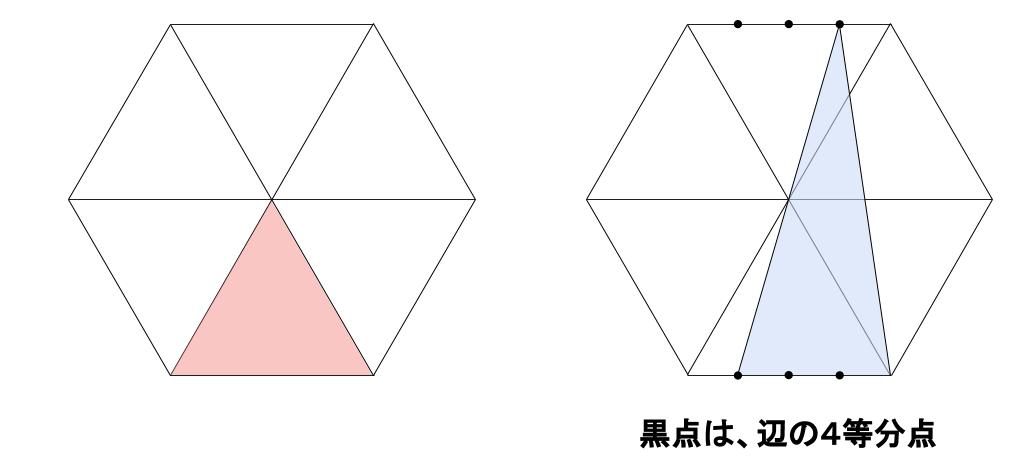

小正三角形と比べて、
底辺は \(\displaystyle \frac{3}{4}\) 倍
高さは2倍よって、25× \(\displaystyle \frac{3}{4}\) ×2=37.5 (\(cm^2\))
ですね。
はい、正解です。
(3)
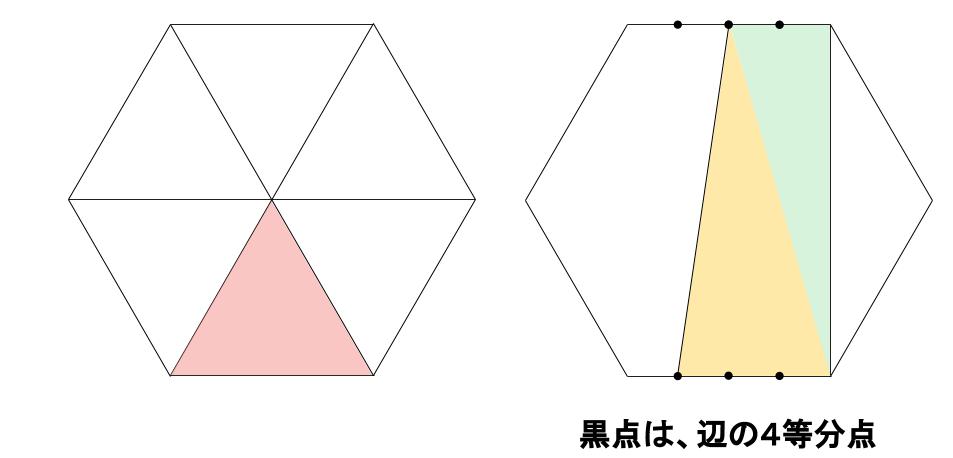

黄色の三角形と
緑の三角形に分けます。
黄色の三角形は、
小正三角形と比べて、
底辺は \(\displaystyle \frac{3}{4}\) 倍
高さは2倍よって、25× \(\displaystyle \frac{3}{4}\) ×2=37.5 (\(cm^2\))
緑色の三角形は、
小正三角形と比べて、
底辺は \(\displaystyle \frac{2}{4}\) 倍
高さは2倍よって、25× \(\displaystyle \frac{2}{4}\) ×2=25 (\(cm^2\))
これらを合わせて、
37.5+25=62.5 (\(cm^2\))
はい、正解です。
