正三角形・その９2018つくこま

正三角形の内部の点からの垂線

解説

この問題は、あることを知っている人から見れば、「知識問題の一種」なのです。

あること？

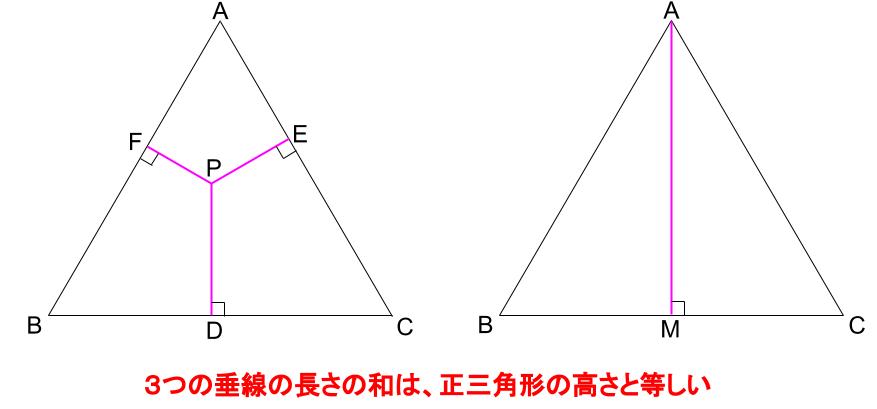
正三角形ABCの内側に点Pがあり、Pから辺BC、AC、ABにそれぞれ垂直な線を引きます。これら３つの垂線の和は、正三角形ABCの高さと等しい。

点Pがどこにあっても一定です。

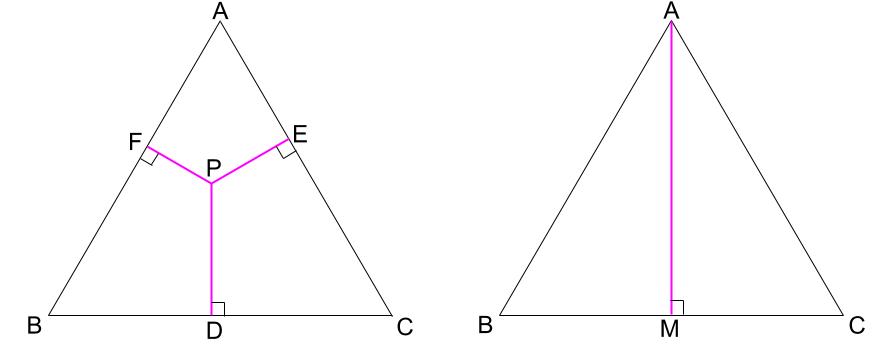
点Pがどこにあっても、
PD+PE+PF=PM
が成り立つと。

はい。
そして、これがなぜ成り立つのか。
面積からわかります。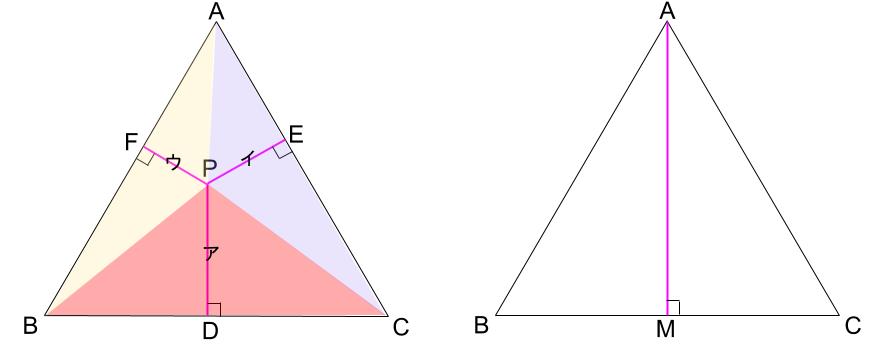

正三角形の１辺の長さをaとします。
赤い三角形の面積は、a×ア÷２
青い三角形の面積は、a×イ÷２
黄色い三角形の面積は、a×ウ÷２
これら３つの三角形の面積の和は、
a×（ア＋イ＋ウ）÷２
もちろんこの面積は、正三角形の面積（a✕「正三角形の高さ」÷２）と等しいので、
a×（ア＋イ＋ウ）÷２＝a×「正三角形の高さ」÷２
よって、
ア＋イ＋ウ＝（正三角形の高さ）
これで示せました。

点Pは辺上にあるときでも成リたちます。
ア＝０ということです。

さて、高さの和が一定になるという事実を知っている人がこの問題を見ると・・・
この問題は似ています。
３つの長さの和（AF+BD＋CE）も、点Pの位置がどこにあっても一定になるのでは？
という予想が可能です。

確かに・・・似てますね・・・

「点Pの位置がどこであっても、３つの長さの和が一定になるのか」
これを、軽く調べてみましょう。
１辺の長さが５の正三角形でちょっと調べてみると・・・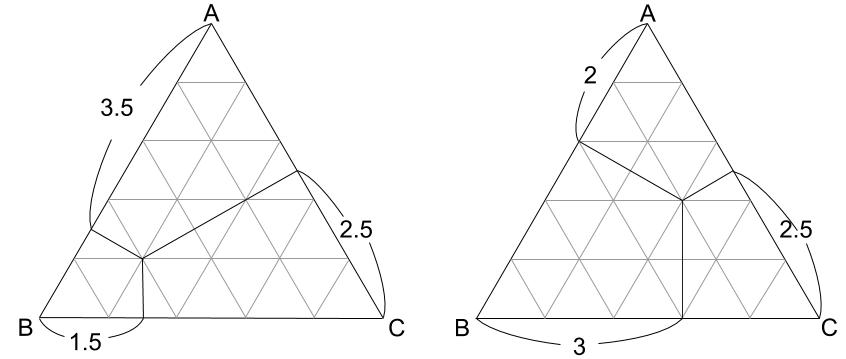

どちらの場合も３つの長さの和は7.5です。

正三角形の１辺は５なので、
(３つの長さの和)：(正三角形の１辺)＝7.5：５＝３：２

点Pがどこにあっても、３：２が成り立ちそうです。

上のようにたった２つの具体例で成り立つからといって、あらゆる場合で成り立つとは言えません。論理に穴があります。
しかし！
入試本番の時間がない中、小学生が解く論理です。
数学的に完璧な論理は無理でも、上のレベルの推論で解答欄をうめることを否定できません。

(３つの長さの和):(正三角形の１辺)＝３：２ならば、

(３つの長さの和)＝７＋８＋10＝25(cm)
なので、
(正三角形の１辺)＝25✕\(\displaystyle \frac{2}{3}\)=\(\displaystyle \frac{50}{3}\)(cm)

はい、これで正解です。
実は、(３つの長さの和):(正三角形の１辺)＝３：２という予想は正しいのです。

ちなみに、「点Pの位置によらず、３つの長さの和が一定になる。」がわかっていれば次のような論理でも解けます。
問題の図を鏡に映します。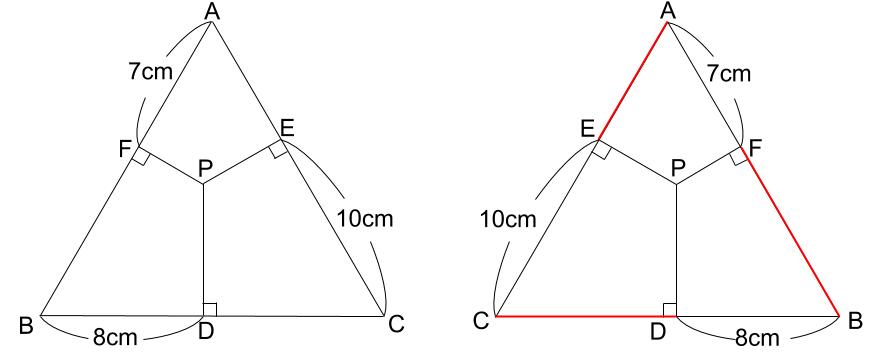

赤い３つの長さの合計も25ｃｍになるので、
正三角形の3辺の長さの合計が、25＋25＝50（ｃｍ）
より、正三角形の１辺の長さは、50÷３＝\(\displaystyle \frac{50}{3}\)(cm)

求まりました。

今回出てきた知識は以下の２つです。
点Pの位置がどこであっても成り立ちます。

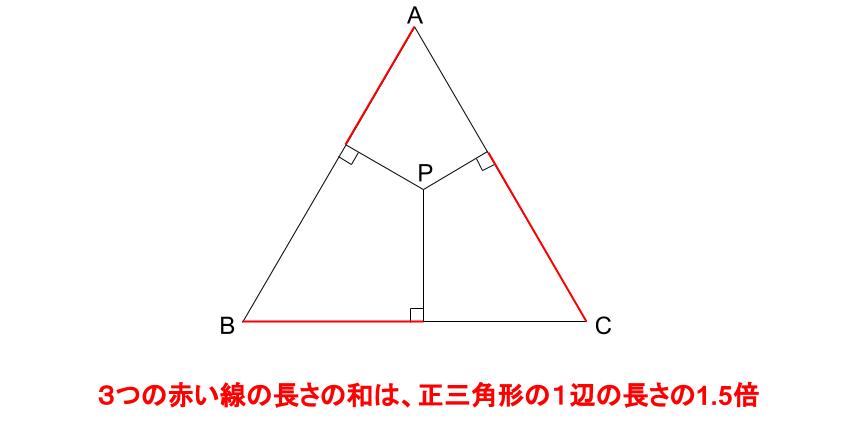
赤い線の長さの和が、１辺の1.5倍になることは次の別解の中で導かれます。

別解

先に紹介した知識なしでこの問題を解くにはどうするのか。
別解として見ておきましょう。

ちなみにこの問題は、筑波大学附属駒場中学校の大問３の（２）として出題されました。
（１）では二等辺三角形の内部に点Pがある問題でした。
（１）のあとに（２）を解くと、次の図のような補助線を引きたくなる流れでした。
出題者もそれを意図していたはずです。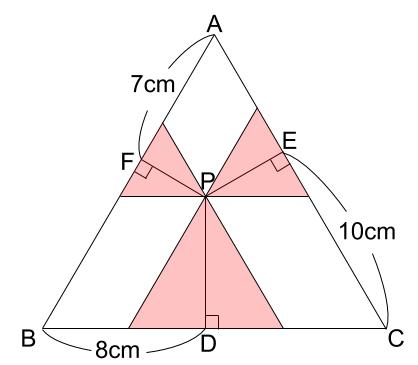

Pを通り外部の正三角形の辺に平行な３本の線を引きました。

すると、正三角形ABCの内部に小正三角形が３つできることがわかります。
他の白い部分は平行四辺形です。

つまり、同じ長さがたくさんあることがわかります。

３つの小正三角形の１辺の長さをそれぞれ、②、２、△２とすると次の図のようになります。

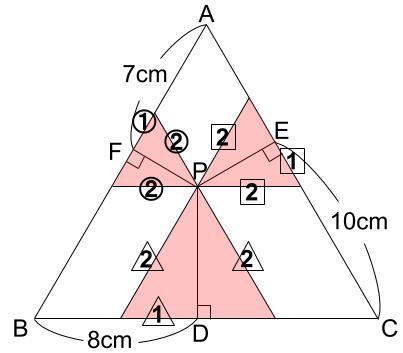
また平行四辺形の辺の長さにも注目します。

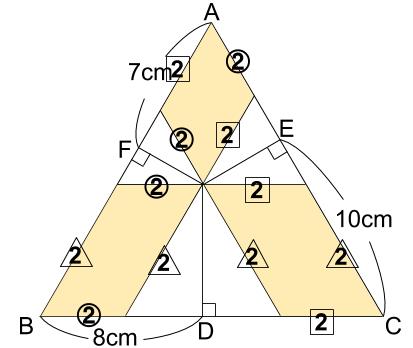
上図より、
①＋２＝７(cm)
②＋△１＝８(cm)
１＋△２＝10(cm)

これらをすべて足すと、
③＋３＋△３＝25(cm)

ところで、正三角形の１辺の長さは上の図から、
②＋２＋△２です。
これは、③＋３＋△３＝25(cm)の\(\displaystyle \frac{2}{3}\)倍です。
25×\(\displaystyle \frac{2}{3}\)＝\(\displaystyle \frac{50}{3}\)(cm)

求まりました。