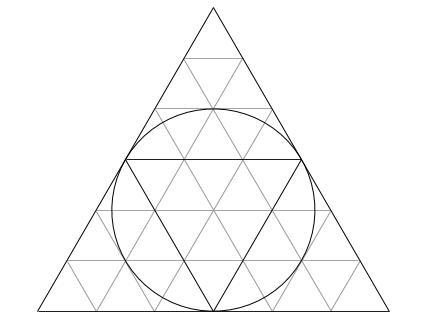
正三角形の重心
- 例題7
-
円の内側にある図形をA、円の外側にある図形をBとします。
Aは正三角形で、Bは正三角形から正三角形をとりのぞいた図形です。
Aの面積はBの面積の何倍であるか求めなさい。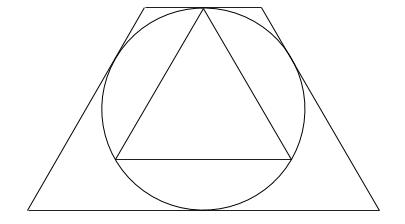
- 解説
-

もちろん、とりのぞかれた正三角形をもとに戻します。
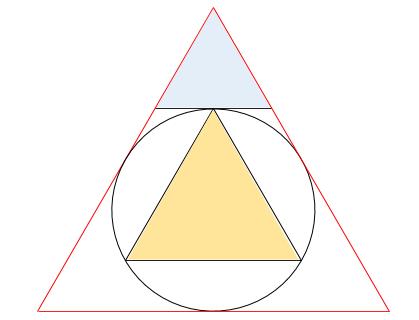

いつものとおり、円の中心から補助線を引きます。
重心が関係した図になりますね。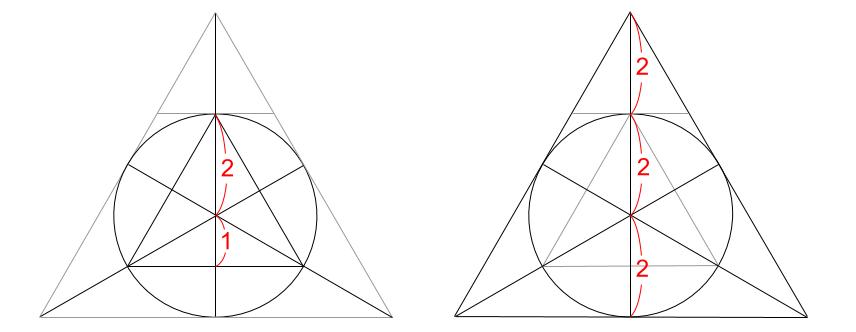

大、中、小。
3つの正三角形の面積の比較です。正三角形の高さの比から相似比がわかりますね。

図より、
大正三角形の高さは6
中正三角形の高さは3
小正三角形の高さは2これらの面積比は
(6×6):(3×3):(2×2)=36:9:4A(円の内部の中正三角形)は9
B(円の外部の大-小)は、36-4=32よって、Aの面積はBの面積の \(\displaystyle \frac{9}{32}\) 倍です。

正解です。
やはり重心の知識がポイントでしたね。参考図

Aを180度回転すると、次の図のようになっています。
小正三角形への分割の有効性も見て取れますね。