正三角形の重心
- 例題6
-
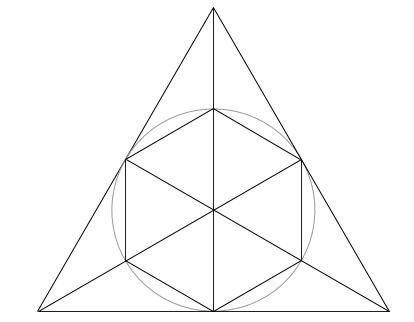
円の内側にある正六角形をA、円の外側にある正三角形をBとします。
Bの面積はAの面積の何倍であるか求めなさい。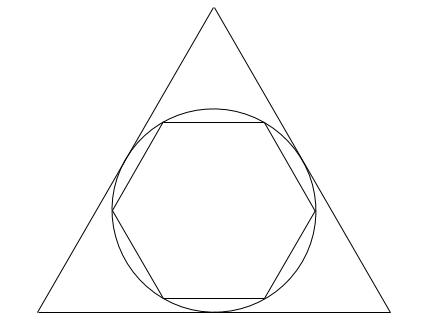
- 解説
-

正六角形と正三角形の面積の比較です。
もちろん正六角形を、6つの小正三角形に分けます。
結局は、正三角形の相似比を求める問題であると理解することが第一歩です。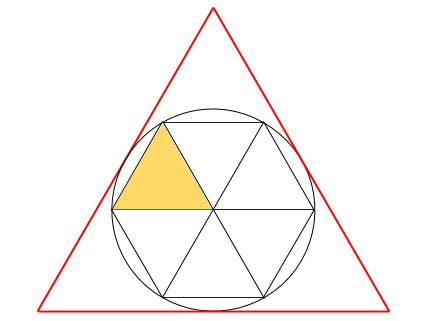

小正三角形の1辺は、円の半径と等しい。
円の半径の長さを1としてみましょうか。
とりあえず、円の中心から補助線を引くことを第一に考えますよね。
やはり重心なんですね。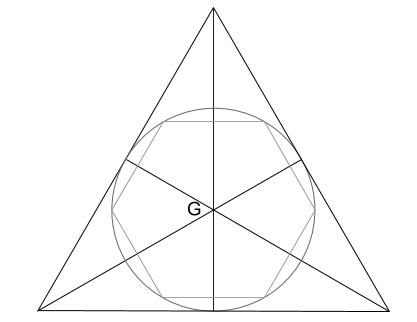

「重心」の図を知っていれば、今回もそれが関係ありそうだなと予想できますね。
そして、長さの比が2:1という知識も使えますね。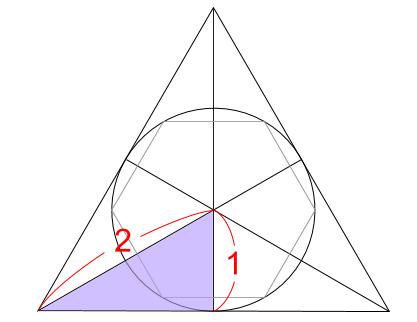

紫色の直角三角形は、1辺の長さが2(円の半径の2倍)の正三角形を半分にした直角三角形です。

つまり、外側の正三角形の面積は、紫色の直角三角形6つ分だから、
1辺の長さが2の正三角形3つ分です。1辺の長さが1の正三角形の面積を①とすれば、
1辺の長さが2の正三角形の面積は④よって、
A(円の内部の正六角形)の面積は、①×6=⑥
B(円の外部の正三角形)の面積は、④×3=⑫
よって、Bの面積はAの面積の2倍です。
はい、正解です!
別解

図形Aを円の中で30°回転させると次の図のようになります。

図形Bが12個の三角形に分割されます。
この12個の三角形の面積がすべて等しいことから解決できます。
