正三角形の高さ
- 例題8
-
下の図において、OCの長さを求めなさい。
また、三角形OABの面積と三角形ODEの面積の比を最も簡単な整数の比で求めなさい。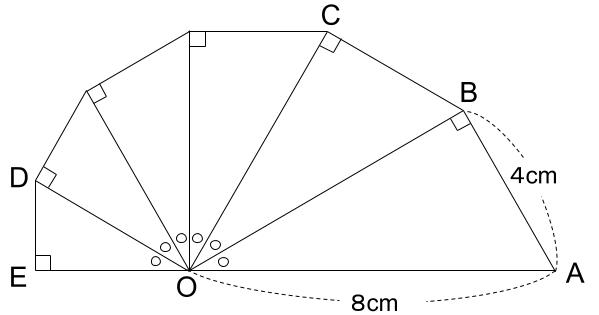
- 解説
-
OCの長さ

三角形OABですが、直角三角形で、8cmと4cm。
1辺が8cmの正三角形の半分です。
つまり、◯の角の大きさは30度。
三角形OABと相似な三角形が、うずまきのように並んでいますね。
OCの長さ・・・まったくわかりませんね。
BからOAに垂線を引いてみたく・・・ならないかな?
結局これも知識なんですよね。知っているから引くべき補助線が見える。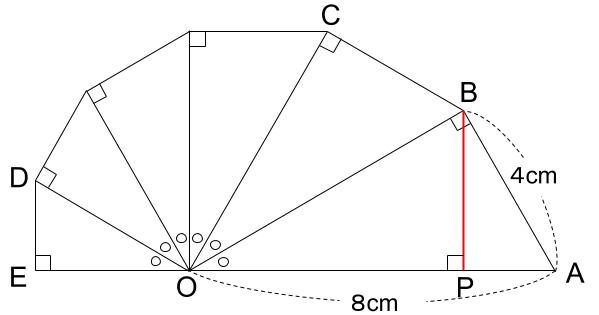

なるほど!直角三角形の相似ですね。
新しくできた直角三角形も、正三角形の半分。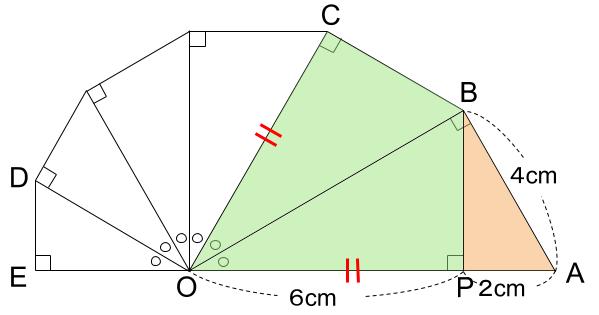

APは、BAの半分で2cm。
OPは、8−2=6(cm)
そして、緑色の三角形は合同です。
わかりました。
OC=6(cm)
はい、正解です。
面積比

では続いて面積比だね。

となりあう直角三角形の面積比が4:3ですね。
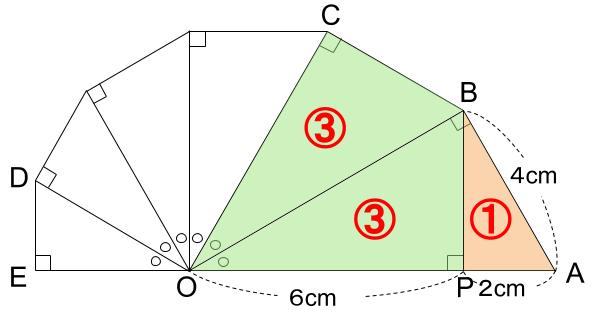

\(\displaystyle \frac{3}{4}\)倍をくりかえしていく。
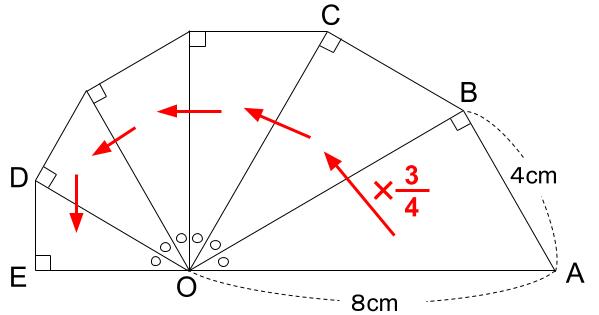

(三角形OABの面積)×\(\displaystyle \frac{3}{4}\)×\(\displaystyle \frac{3}{4}\)×\(\displaystyle \frac{3}{4}\)×\(\displaystyle \frac{3}{4}\)×\(\displaystyle \frac{3}{4}\)=(三角形ODEの面積)
つまり、
(三角形OABの面積)×\(\displaystyle \frac{243}{1024}\)=(三角形ODEの面積)
よって、求める面積比は、1024:243です。
はい、正解です。
正三角形の分割

さて、この問題におけるはじめの補助線。
直角三角形を相似な直角三角形2つに分割しましたが、
これは、どんな直角三角形に対しても行われる大事な分割です。
そして、正三角形を半分にした直角三角形においても、大事な分割です。
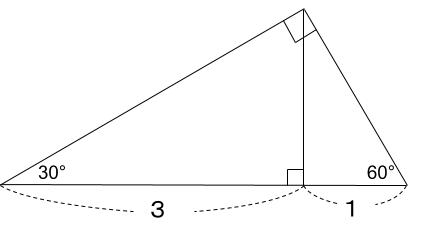

垂線によって、辺が3:1に分けられます。
これも覚えておいた方がよい重要図形です。ちなみに、次の図のように合同な4つの直角三角形に分割も可能です。
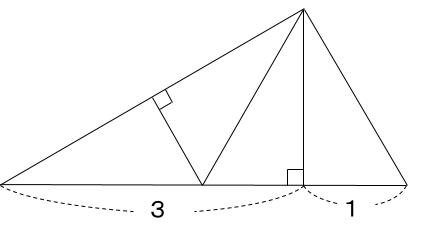

なんだかきれいな分割ですね。

これは今までにでてきた有名図形配置とも強く関連しています。
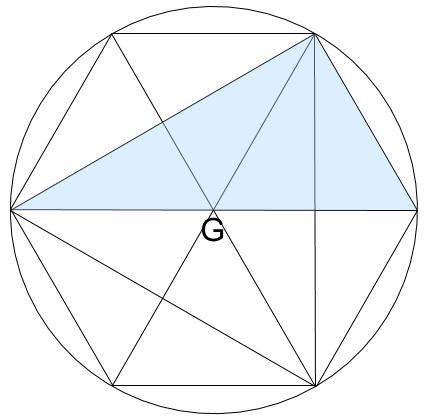

正三角形の重心とも関係あるのですね。

はい。このような有名図形配置をもとにして作られる問題は多いのです。
しっかり覚えておきましょう。正三角形の高さ

さて、今見てきた図形を用いて、正三角形の高さについても学習しておきましょう。
1辺の長さが2cmの正三角形の高さをアcmとします。
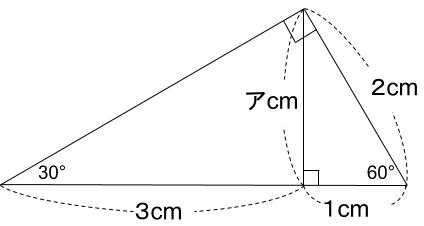

相似な直角三角形の辺の比に着目すると・・・
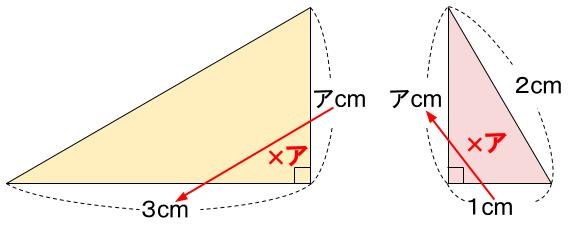

ア✕ア=3
であることがわかります。
直角をはさむ辺の長さの比が1:ア
アcmをア倍すると3cmになる。
だから、ア✕ア=3ということですね。
はい。
アはどんな値なのかというと、
ア=1.732・・・
永遠に終わらない小数です。
くりかえしもないため、分数で表示できない値なのです。
正式に習うのは中学生になってからです。
小学生の学習範囲外ということです。
だから、正三角形の高さが積極的に話題になることはありません。
でもね・・・
これを知っていたら楽に解ける問題、実際に出題されています。
正三角形の高さに関する知識が、そのまんま出題されたこともあります。
「1辺の長さが2cmの正三角形の高さをアcmとする。
このとき、1辺の長さがアcmの正方形の面積を求めなさい。」
このような、そのまんまの問題が出題されたこともあります。
答えは、ア✕ア=3より、3 \(cm^2\) です。
※問題文は上とは違います。例えば、渋谷教育学園幕張中学校で出題されました。
※今回の例題8も、正三角形の高さの知識から解くことも可能です。
