1:つるかめ算
なかでも、もっとも有名なものが「つるかめ算」ではないでしょうか。
つるかめ算は他の文章題の中で1つの計算技術として使われることになります。
必ずマスターしなければならない特殊算です。
※理科の計算問題の中でも必要となります。
1:つるかめ算と具体図
例題1
ツルとカメがあわせて13ひき(羽)います。足の数はぜんぶで36本です。
ツルは何羽いますか。カメは何ひきいますか。
※ツル1羽の足は2本、カメ1ひきの足は4本ですよ。
解説

さて、今日学習するのは、かの有名な「つるかめ算」です。聞いたことある?

あるような。ないような・・・

では「つるかめ算」を生まれて初めて見る学くん、さっそくなんだけど、とにかく問題を解いてみてください。。
習ってないからできません!
ではなくて、いろいろトライしてみてね。

そんなこと言っても・・・うーん
スパッと解けないでしょ。どうやって答えにたどりつこうか、というパズルとしての楽しさを
伝えたい問題です。
あてはめで解く
問題にでてきた数、13、36、2、4を適当にくみあわせて計算してるだけの子は要注意です。
算数と向かい合っていません。なんとなく計算をして、なんとなく答えをかく、このような計算をしても、まったく意味がないと強く指導しないといけません。
一方、あてはめで答えを探すアプローチをとった子は大いに褒めてあげてください。
「問題の意味がわかり、どうやれば答えを探し出せるかがわかる」ということは素晴らしい算数力です。
もっとうまく解くやり方があるよ、ということは2次的なことなのです。
また、まったく解き方がわからないで手が動かない子には、あてはめで答えを探すことをうながしましょう。

いつもいつも、きれいに計算で答えがでるとは限らないんだよ。

?えーっと、つまり・・・どういうことですか?

うまくいく答えをひたすら探す、という問題の解き方だってあるんだよ。
やってごらん。

探すといっても・・・何をやったらいいのか分からないです。

むむむ!そうか。
「あてはめて探す」という解き方をやったことがないかな?
この問題の答えの候補は下の表の14通りの中のどれかなんだよ。わかる?


あ、はい。わかります。

この14通りのどれかが正しいんだけど、正しいのはどれ?

それがわかったら苦労しません。

では聞き方を変えるけど、この14通りの中のどれが答えになるのか、決め手は何かな?

足の数が全部で36本になるかならないか・・・

そうだよね。はい、探してください!!

14通り、全部調べるんですか?

いやいや、運が良ければ一発で当たるかもしれない。
さあ、運試しだ!

運試しか。よーし。
ツルが10、カメが3ならば・・・
足の合計は、
2×10+4×3=32
32本だ。
あー、不運!!

でもかなりおしいね。36本と近いよ。
で、次は運試しじゃないよ。頭を使ってね。
先生から改めて問題だよ。
先生からのヒント問題
足が36本になるようにしたいので・・・ツルが10、カメが3(足の合計32本)ではありませんでした。ツルとカメ、どちらを増やしてどちらを減らせばよいですか。

足を増やしたいんだから・・・
足が多いのはカメ、つまりカメを増やす!
⇒ツルを減らしてカメを多くする!

正解!
ツルを1減らして、カメを1増やすと
ツルが9、カメが4になるね。足の合計はいくつになるかな?

2×9+4×4=34
足は全部で34本です。

正解なんだけど、もっと簡単に求めよう。
ツル(2本)1羽をカメ(4本)1ひきにかえたんだよ。
足の数は何本増えるかな。

2本足のツルを4本足のカメに代えた。
2本増えますね。
だから、32+2=34なんだ!
⇒1ひき交換すると、足が2本増える!!
あ!!ということは・・・
あともう1ひきツルをカメに代えれば、34+2=36になる。
つまりツルが8羽、カメが5ひきのときに、足が合計36本だ。
これが答えです。ツルが8羽、カメが5ひきです。

正解かどうか、計算して確かめられますね。
ツルが8羽、カメが5ひきのときの足の合計は、
2×8+4×5=36
確かに36本。
うまくいっていますね。
正解です!
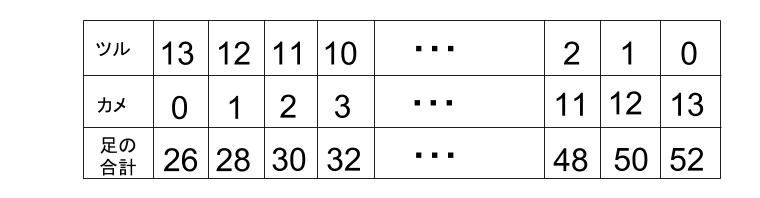
ところで、ツルとカメの合計が13ひきのとき、下の表のような全14通りが考えられるんだったよね。ツルを1減らして、カメを1増やすと、足は2ずつ増えることが見てとれます。
具体図で整理する

「ツル⇒カメ」の交換で足が2本増えるという話なんだけどね。そんなの当たり前だと思っているかもしれないけれど、腹の底から実感するために、目で見てわかっていただこうと思います。この問題は「具体図」で表すのがぴったりだと思いませんか。


なるほど。目で見てわかりました。
交換したツルとカメ以外は、まったく変化なしですからね。
納得です。

さて、さっきは運試しで、カンで調べ始めました(ツルが10、カメが3)。
カンで一発で正解することもあまりなさそうですし、スタート地点は「ツルが13、カメが0」とするのがおススメです。
「もし全部ツルならば」という解法です。
足の数の合計が何本なのかを計算するのが非常に楽ですよ。
これで先ほどの問題をもう一度解いてみてください。
もし~ならば 「仮定」という高級な考え方ですね。
もちろん、「もしツルが10、カメが3ならば」も仮定です。

具体図で解いてみます。


足を10本多くするためには、
10÷(4-2)=5
ツル5をカメ5に代えないといけない。
つまりカメは5ひきいます。
13-5=8
ツルは8います。
なるほど。すごいスッキリ解けましたよ。

うん、素晴らしいね。
ツルとカメの1ひきあたりの差である2を集める解き方だよ。
つるかめ算は、面積図で教えられていることが多いです。
しかし、すぐに面積図を指導することはおススメいたしません。
面積図は抽象度が一段階高い図です。具体図での解法を腹の底から理解した後に、面積図へと移行していくべきです。
