正三角形その１０2018海城

正三角形の辺上の点からの垂線

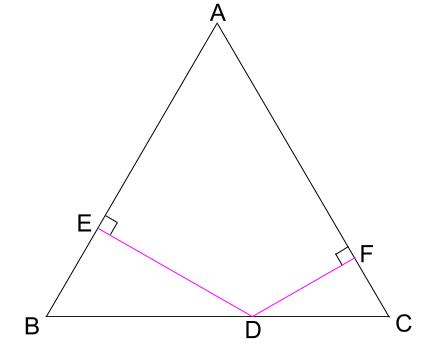
解説

前問とそっくりですよね。
同じように解くことになります。

正三角形の内部からではなくて、辺上から

前問では正三角形の内部の点P。
今回は、点Pが辺上にあるようなものです。
点Pが辺上にあっても、前回学んだ性質は成り立ちます。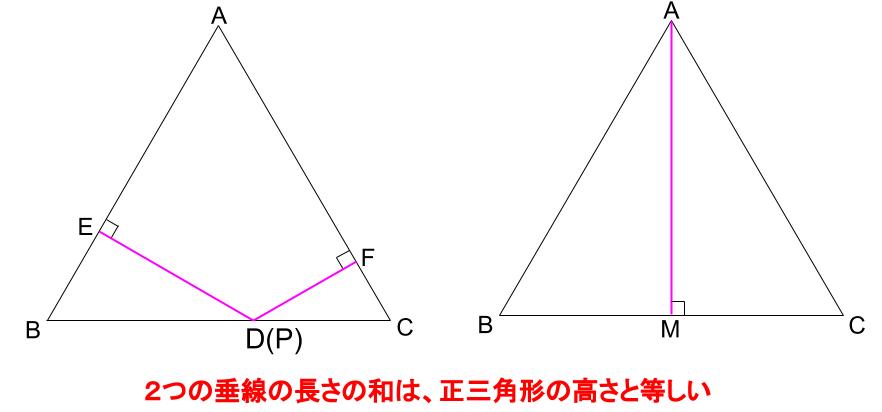

垂線の長さの和は、正三角形の高さと等しい。
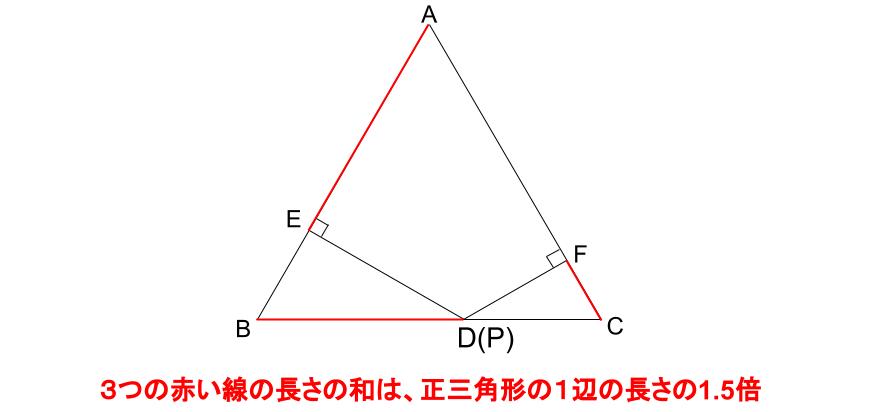
それから発展して、
AE＋BD＋CF=（正三角形の１辺）✕1.5
も成り立つ。

そうですね。知っていれば一瞬で解けるタイプの問題です。
このタイプの問題は海城中学校をはじめいろいろな学校で実際に出題されてきました。

AE＝７cm
BD＋CF=８cmなので、
AE＋BD＋CF=（正三角形の１辺）✕1.5
15＝（正三角形の１辺）✕1.5
（正三角形の１辺）＝10cm
求まりました。

はい、正解です。

別解

知識なしで解くならば、次の図のような補助線で正三角形と平行四辺形をつくります。

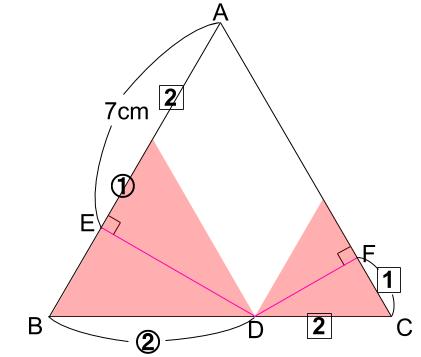
①＋２＝７cm
②＋１＝８cm
あとはこれらの式を変形をすれば解けます。

上の２つの式を足すと、
③＋３＝15cm

式全体を\(\displaystyle \frac{2}{3}\) 倍すると、

②＋２＝10cm

辺BCの長さは、②＋２なので、
正三角形ABCの１辺の長さは10cmと求まりました。

あるいは、普通に消去算です。
①＋２＝７cm
②＋１＝８cm
これらから、
①＝３cm、１＝２cm
と求まります。