正三角形の重心
- 例題5
- 面積が24 \(cm^2\) の正三角形ABCがあり、その中心をOとます。Oを中心として、正三角形ABCを時計回りに60°回転した図形を正三角形DEFとします。このとき、正三角形ABCと正三角形DEFが重なった部分の面積を求めなさい。ただし、中心Oは、OA=OB=OCを満たす点とします。
- 解説
-

なんと、この問題にはあらかじめ与えられた図がありません。
ですから自分で作図して解くことになります。
実際に星光学院中学校で出題された問題です。
文を読んで図を書く・・・
どんな図をかけばいいのか
もちろん作図のポイントは中心Oです。
「正三角形ABCの中心Oは、OA=OB=OCを満たす点」
と問題文にあります。もちろん、正三角形ABCの中心Oとは、重心のことです。

確かに・・・そうなる・・・のかな?

「重心を中心として、正三角形ABCを時計回りに60°回転」とあるので、
重心を知っている生徒ならば、迷うことなく次の図までかけるでしょう。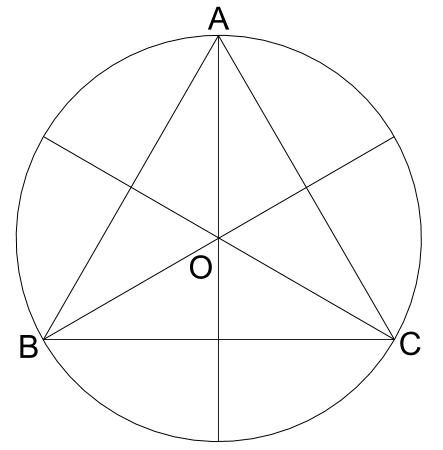

何も知らない状態で、試験会場で、図形の性質を考えながらこの作図をすることはかなり厳しいですね。
時間制限がありますからね。つまり、この正三角形と重心にまつわる基本的な図形的性質を暗記しておくべきなのです。
入試本番までに学習を済ませておいてから、この問題に臨むべきなのです。出題した中学校の数学の先生もそう思っているはずです。

確かに。
知っている子と知らない子では圧倒的な差がつきますね。
そうです。ですから、重要な知識は持っておくべきなのです。
さて、続きです。正三角形ABCを60度回転させます。
正三角形ABCと正三角形DEFが重なった部分は、次の図のように六角形です。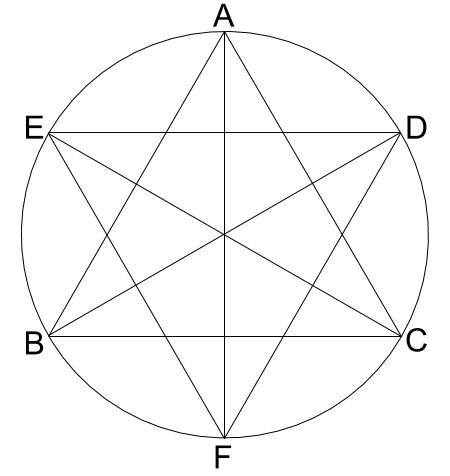

これは正六角形かな・・・

正六角形ならば、最も有名な分割は、正三角形6つの分割です。
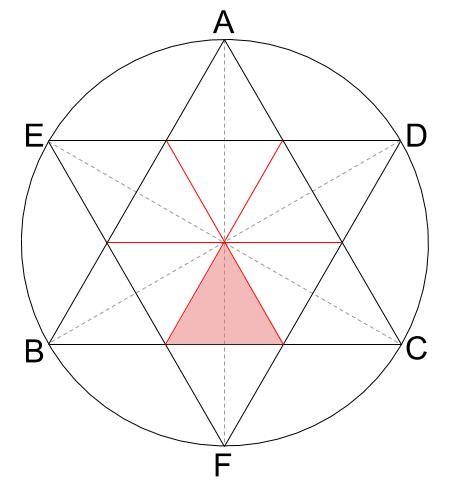

お!
すごくきれいですね!
すると、小正三角形が12個になります。
この12個の正三角形の高さがすべて等しいですね。
正三角形の高さは、円の直径の \(\displaystyle \frac{1}{4}\) であることが確認できます。
正三角形ABCの面積が24 \(cm^2\) で、小正三角形9個にわれています。
そして、重なりは6個分です。よって、正三角形ABCと正三角形DEFが重なった部分の面積は、
24× \(\displaystyle \frac{6}{9}\)=16 \(cm^2\)
求まりました。

正解です。
