正三角形とおうぎ形
- 例題2−1
-
下の図は点Aを中心とする半径6cmの円と、点Bを中心とする半径6cmの円を組みあわせたものです。
水色の部分の面積を求めなさい。
ただし、円周率は3.14とします。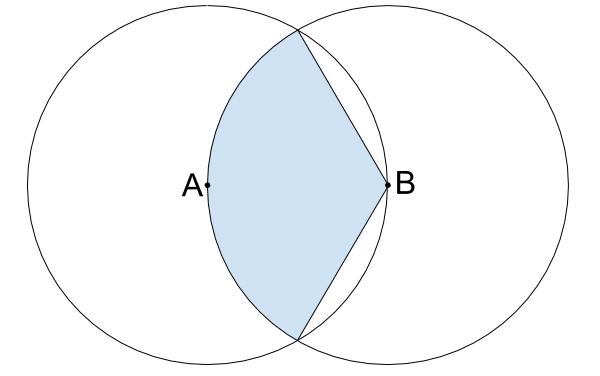
- 解説
-

これも正三角形の作図と同じコンパスの使い方ですね。
正三角形が2つあります。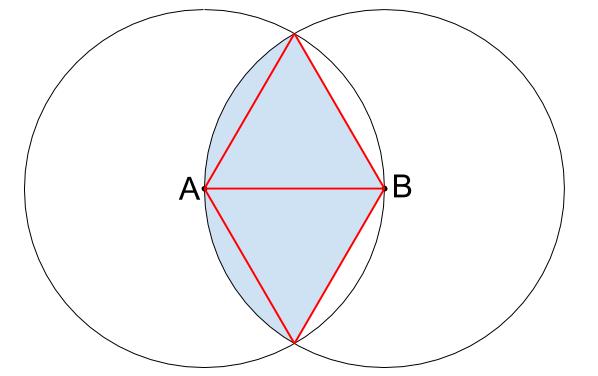

つまり、水色の部分は中心がBのおうぎ形で、中心角が120度。
その面積は、
6×6×3.14×\(\displaystyle \frac{120}{360}\)=37.68 \(cm^2\)

正解です。
- 例題2−2
-
下の図は半径6cmの円3つを、互いの中心を円周が通るように重ねたものです。
水色の部分のまわりの長さを求めなさい。
ただし、円周率は3.14とします。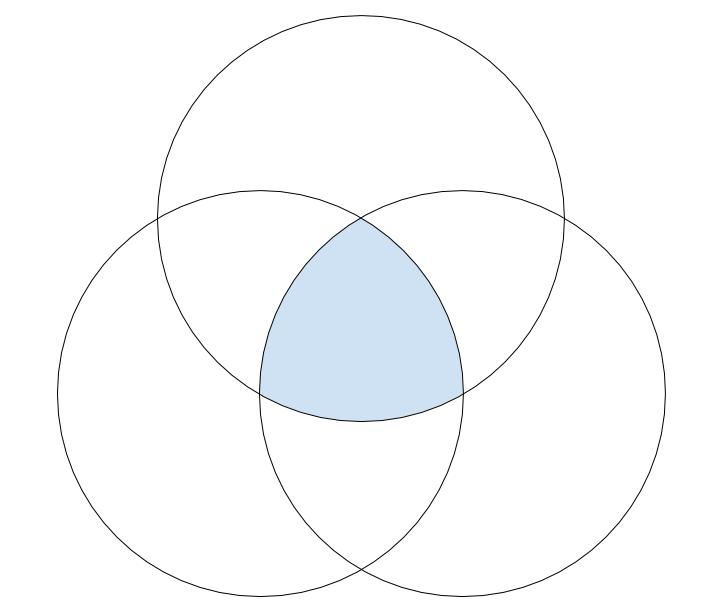
- 解説
-

同じように正三角形がカギになるわけですね!
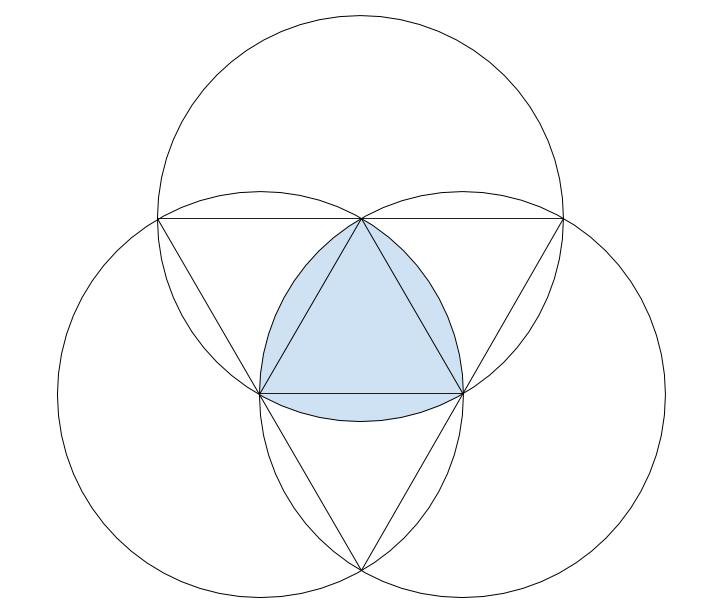

この図形のまわりは3つの曲線で囲われていて、1つ分の長さは、60度のおうぎ形の弧の長さ。
よって、
6×2×3.14×\(\displaystyle \frac{60}{360}\)×3=18.84 \(cm\)

正解です。
あとね、円と正六角形、さらに正六角形を6つの正三角形に割った配置は
絶対に暗記しておかないといけない有名配置です。
次の図の赤い円、正三角形6つです。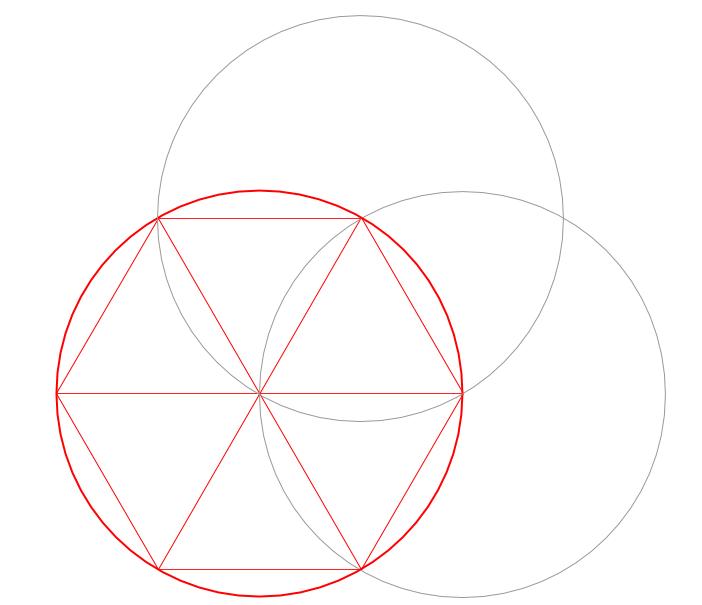

中心角が120度や150度のおうぎ形の作図をして解く問題もあります。
120度や150度は、円と正三角形の有名配置を背景に作図するのです。
円すいの展開図を考える問題などが代表例です。
そのとき、図の中に正三角形を見つけ出して解くことが多いです。
図があまりにも下手で気づけないということが起こらないように、はじめから正三角形を意識しながら作図をすることが大事です。
