正三角形に関する重要知識・その１

正三角形とおうぎ形

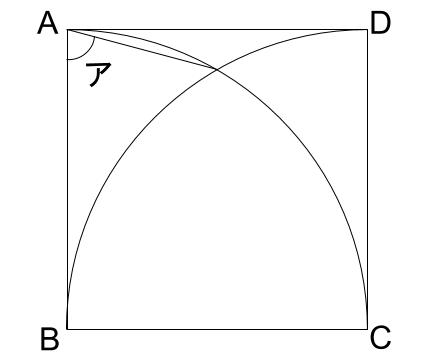
解説

アの角を作っているのは、２つのおうぎ形の交点です。
この交点をPとします。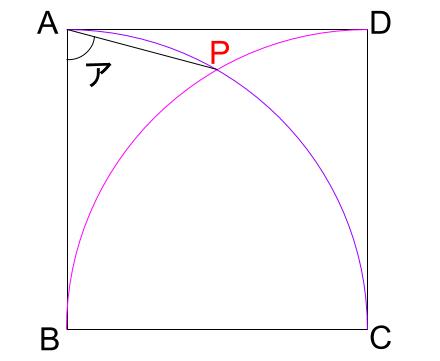

アの角について知りたい。
これはつまり、点Pがどのような位置にあるかを知るということです。

点Pは２つのおうぎ形の交点です。
コンパスを使ってこのような交点の作図ってしたことあるでしょ？

え！？
あるかなあ・・・

絶対にあると思うんですけどね。
これは、正三角形の作図ですよ。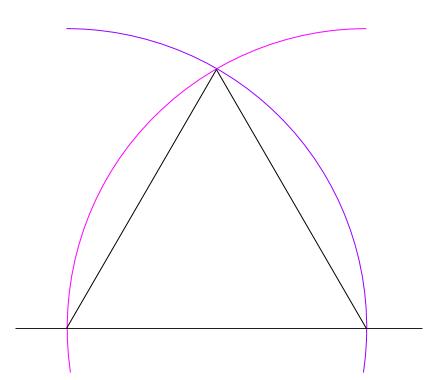

確かに。
やったことあります。
思い出しました。

はい。
有名図形なので、必ず覚えておいてください。

この問題は、正三角形に気づく問題なんです。

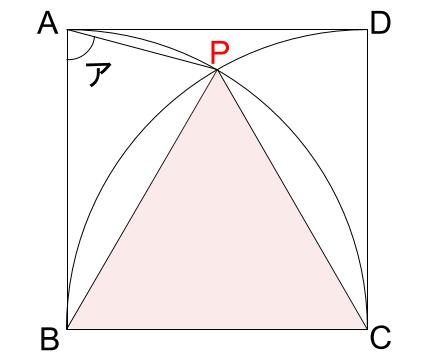
で、角アの大きさですが、わかりますか？

えっと・・・
わからないです。

角度がわからないとき、「二等辺三角形」を探すことも有効です。
特に、「同じ辺の長さ」があるときは二等辺三角形です。

あ！三角形BPAが二等辺三角形だ。

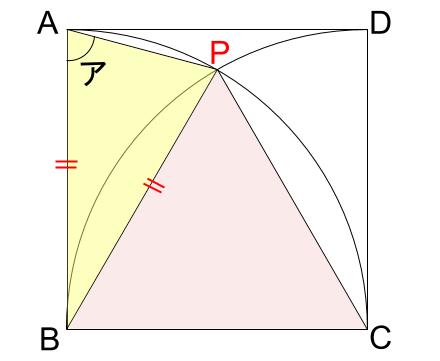
角Bは、90°ー60°＝30°
だから、角アの大きさは、
（180－30）÷２＝75

75°ですね！

はい、正解です。

半径の等しい円を組みあわせることで、正三角形が作られる。
必ず暗記しておかなくてはならない重要ポイントです！