過不足算
長イス
例題1
生徒たちを長イスにすわらせていきました。1脚に5人ずつすわらせると、13人の生徒がすわれませんでした。そこで、1脚に6人ずつすわらせると、最後の3脚には4人ずつがすわり、全員がすわることができました。生徒は何人いましたか。
解説

長イスは過不足算の定番テーマだよ。
「イスに人を配る」のです。
「人に折り紙を配る」のと同じように考えればよいです。

とにかく図にしますね。


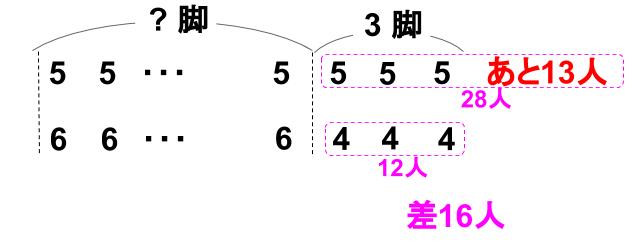
最後の3脚の長イスに生徒を座らせなければ、
5×3+13=28(人)すわれないか、
4×3=12(人)すわれないか、
16人の差が出ます。

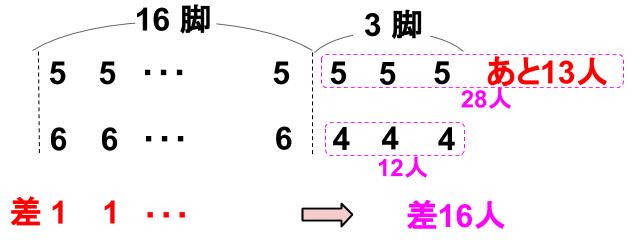
この16の差は、6-5=1
1の差が集まってつくられた差なので、
16脚にすわらせたときにできる差。
つまり、長イスは全部で、16+3=19
19脚ある。

生徒は、
5×19+13=108(人)
であり、
6×16+4×3=108(人)
はい、矛盾ありません。
生徒は108人です。

正解です!
素晴らしいね。

別解も見ておこうか。
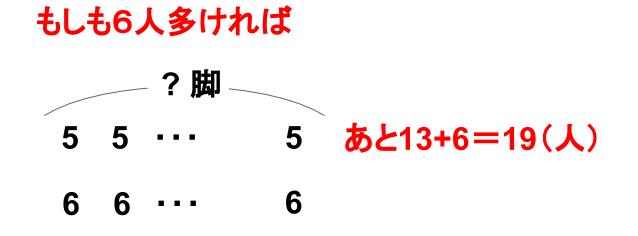
今回は、すべての長イスに6人ずつすわらせることができなかった。
生徒が、もしあと何人多ければ、すべての長イスに6人ずつすわらせることができるだろうか。

3脚が4人ずつになったのだから、
1脚につき2人ずつ追加すればいい。
2×3=6
あと6人多ければ、すべての長イスに6人ずつすわらせることができますね。

あ!
19÷(6-5)=19
長イスが全部で19脚あることがわかりますね。

そういうことです。
あとは計算するだけ。
もし6人多ければ、6×19=114
本当は6人少ないから、114-6=108
人数が108人であることも求まりましたね!
