速さと比
同じ距離を進む
例題1
太郎は学校から駅に向かって、次郎は駅から学校に向かって同時に出発しました。出発から20分後に2人はすれちがい、その16分後に太郎は駅に着きました。次郎が学校に着くのは、太郎が駅に着いた何分後ですか。
解説

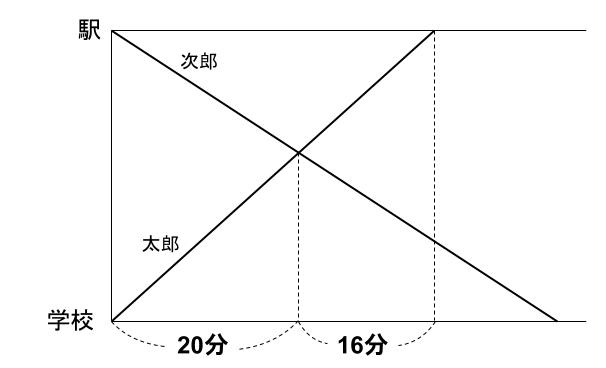
ではダイヤグラムをかいてみますね。

旅人算のような1本の式で処理できる箇所はないね。
このようなときは、比を使うのでしたね。
どことどこを比べればいいのか。
いろいろ考えてみてね。

20:16=5:4だから、これを使いそうだなあって予感はします。
太郎は次郎より速いから
太郎の速さが5で、次郎の速さが4かなあって・・・

まったく手も足もでない問題に、時間をかけられない追い詰められた状況で、そのような当てはめをすることは否定しないけどね。
今はとにかく学力そのものを伸ばしていきましょう。
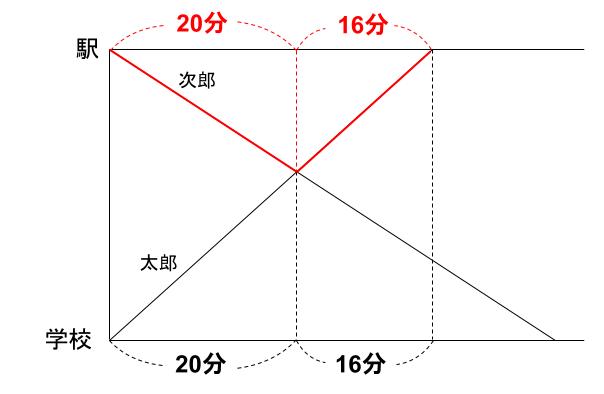
下図に着目するんだよ。
2人の比がわかるよ。

なるほど。同じ距離ですね。
次郎は20分、太郎は16分で進んでいます。
太郎の速さが5、
次郎の速さが4ですね。

その通り。
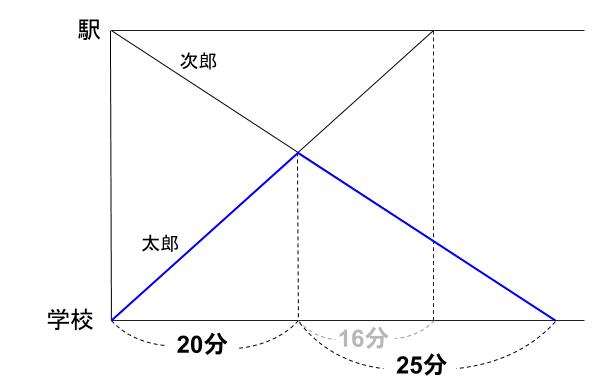
さらに、同じようなものが見つかる。

なるほど!
ここも、同じ距離です!
速さ5の太郎が20分で進んでいる。
速さ4の次郎は25分で進みますね。
5:4の逆比、かかる時間の比は4:5だから。
つまり、次郎は、20+25=45、
45分で学校に着いた。
太郎は36分で駅に着いたから、45-36=9
9分後です

正解です。
ちなみに、「同じ距離」に着目しない別解もあります。
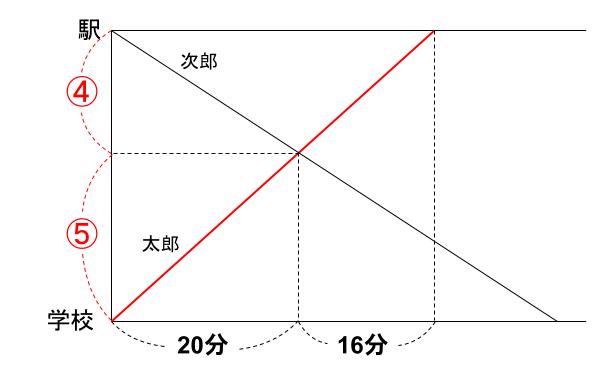
太郎が20分で進む距離と、太郎が16分で進む距離の比は、20:16=5:4
下図のようになり、出会った地点が全体の \(\displaystyle \frac{5}{9}\) であることがわかります。

次郎は④を進むのに20分かかったのだから、
残りの⑤を進むのに25分かかりますね。
これで求まりましたね。
ちなみにこの問題は線分図との相性もいいかな。
次郎が20分かかって進む距離を太郎は16分で進むことに気づきやすい図になりますね。