食塩水の総量に着目する
同時に異なる量の交換・同じ濃さ
例題1
容器Aには5%の食塩水が200g、容器Bには13%の食塩水が600g入っています。Aから60g、Bから何gかの食塩水をくみ出してそれぞれに移しかえると、2つの容器の食塩水の濃度が同じになりました。
(1)この操作の後、食塩水の濃度は何%になりましたか。
(2)容器Bからくみ出す食塩水は何gですか。
解説

さっきは、「同時に、同じ量を交換」して、同じ濃さになる問題でした。
今回は似ているけど・・・
「同時に、異なる量を交換して、同じ濃さ。」

そうだね。
異なる量の同時交換で、等しい濃さになっているね。
もちろん、1つ前の問題と似たような考え方で解決するよ。

今回も、
「交換前をまぜたもの」と「交換後をまぜたもの」が同じですね。
その濃さを求めます。
交換前をまぜたものの濃さは・・・
5%の食塩水が200gと13%の食塩水が600gを混ぜる。
濃さは11%ですね。
※普通に計算しても求まるし、面積図で求めてもよい。

うん正解、さっきと同じだよね。

交換後は、AとBは同じ濃さになった。これらを混ぜたら11%になるのだから、
交換後のAもBも、濃さは11%だとわかります。

うん正解、これもまたさっきと同じだね。

5%の食塩水と13%の食塩水を混ぜて、11%にするには、
1:3 で混ぜるしかない。
つまり、AもBもこの比率でまぜたことがわかります。
容器Aは60gをくみ出した。Aに残っていた食塩水は140g。
だから、Bからやってきた食塩水は、
140×3=420
容器Bから420gを移したことがわかります。
答えは420gですね。

カンペキだよ!正解。
Aでは、
5%の食塩水140g
13%の食塩水 420g
この2つを混ぜて、11%にした。
Bでは、
5%の食塩水60g
13%の食塩水180g
この2つを混ぜて、11%にした。
これがこの問題のすべてだね。
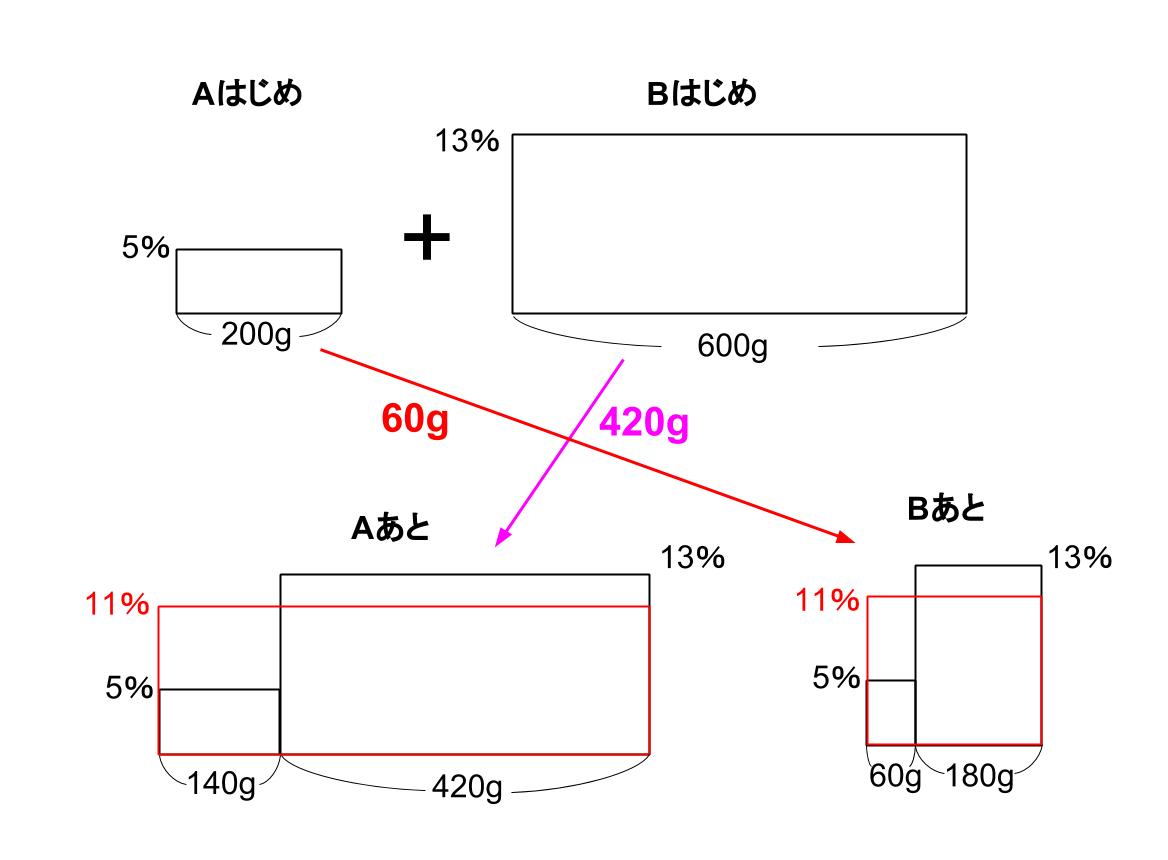

AもBも1:3で混ぜてます。
うまくいってますね!
