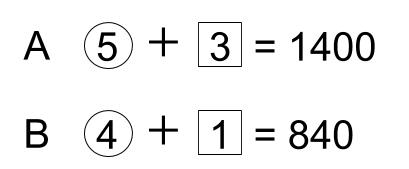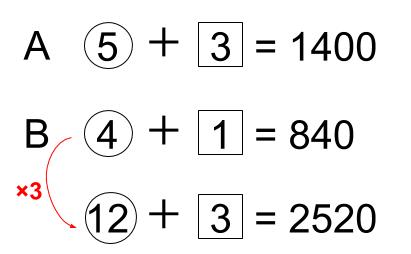異なる2種類の比の処理
問題中に異なる2つの比があるとき。共通部分で比をそろえて解くのが定番パターンでした。しかし、共通部分がない問題もあるのです。それらを見ていきましょう。
共通部分がなく連比ができないパターン
例題1
AとBの所持金の比は5:4でしたが、AもBもおこづかいをもらいました。2人がもらったおこづかいは、AがBの3倍でした。するとAの所持金は1400円、Bの所持金は840円になりました。Aのはじめの所持金はいくらですか
解説

2種類の比に共通部分なし。
「差一定」なりたたず。
「和一定」なりたたず。
さすがに消去算ですよねっ!

はい、その通りです。
今までの知識がきちんと頭の中で整理されているようだね。
今回は素直に消去算をしましょうかね。

はい!

下の式を3倍して、□をそろえます。

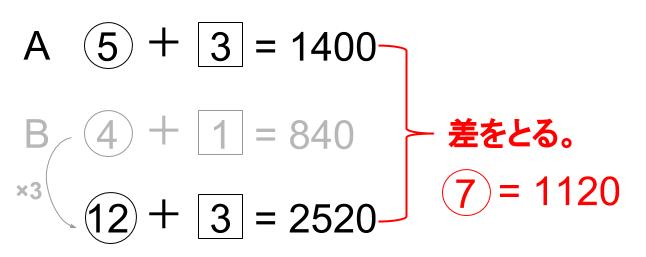
下から上を引けば、3はちょうど消えます。

⑦=1120
だから、
①=160
つまり、Aのはじめは、⑤=800円!

うん、大正解!
しっかりこの定番パターンを覚えてね!
今回は□をそろえて解いたけど、もちろん○をそろえたって同様に解けるよ。
ちなみにAのはじめの金額以外もすべて求められるね。
A:800+600=1400
B:640+200=840