通過算
定番から外れたものは絶対に図示せよ

では通過算の「定番外し」の問題を見ていこう。
いずれも、図をかいて対応します。
図のどこに着目すればよいのかについては、「定番パターン」と同じようになるから、定番パターンの図をどれだけかいてきたか、練習量がものを言うんだ。
例題1
長さ160mで秒速20mの列車Aが、長さ340mのトンネルを通過します。列車A全体がトンネルに入っている時間は何秒間ですか。
解説

確かに、定番パターンとは違いますね。

うん。だから、必ず図をかいて確認しながら解くんだ。

下図のようになりますね。
最後尾に着目した図です。
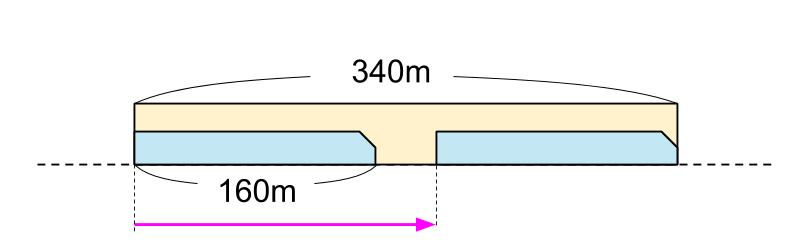

素晴らしい図です。あとは計算するだけだね。

列車Aの最後尾は、340-160=180(m)進んだ。
列車Aは秒速20mだから、
180÷20=9
答えは9秒です。

大正解!基礎がきちんと身についているようだね!
例題2
長さが160mで秒速20mで走る列車Aの先頭が、長さ240mの列車Bの最後尾に追いついてから30秒後、列車Aの先頭が、列車Bの先頭に追いつきました。列車Bの速さは、秒速何mですか。
解説

確かに、これも定番パターンとは違いますね。

うん。だから、必ず図をかいて確認しながら解くんだ。

図は下図のようになりますね。
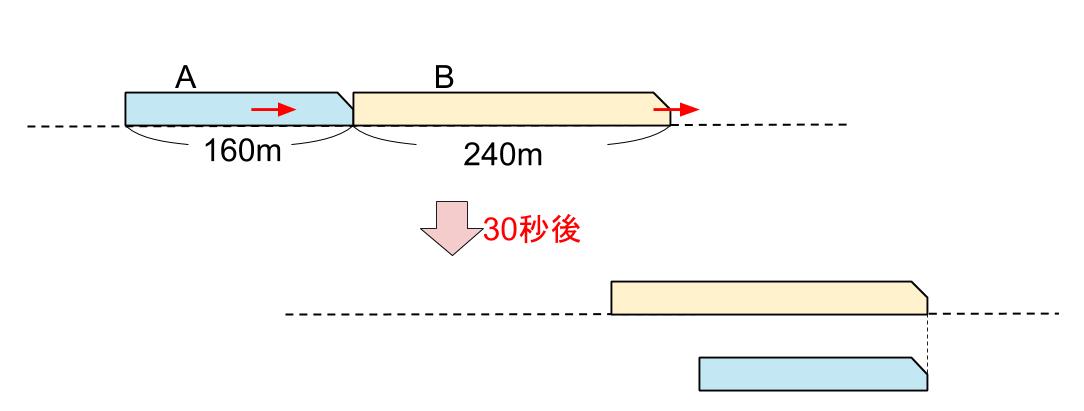

で・・・えっと。
どこがポイントかな・・・

素晴らしい図だよ。この図のどこに着目すればよいか。
それは、今までたくさん練習してきた「定番パターン」と同じなんだ。
「通過が終わったときに、同じ地点にあるもの」に着目しようね。
定番パターンの練習が足りていないことが分かったならば、急いでこれから先に進んではいけません。
もどって基礎からやりなおしましょう。

Aの先頭がとBの先頭が同じ地点にいますね。
Aの先頭とBの先頭に着目して旅人算ですね!
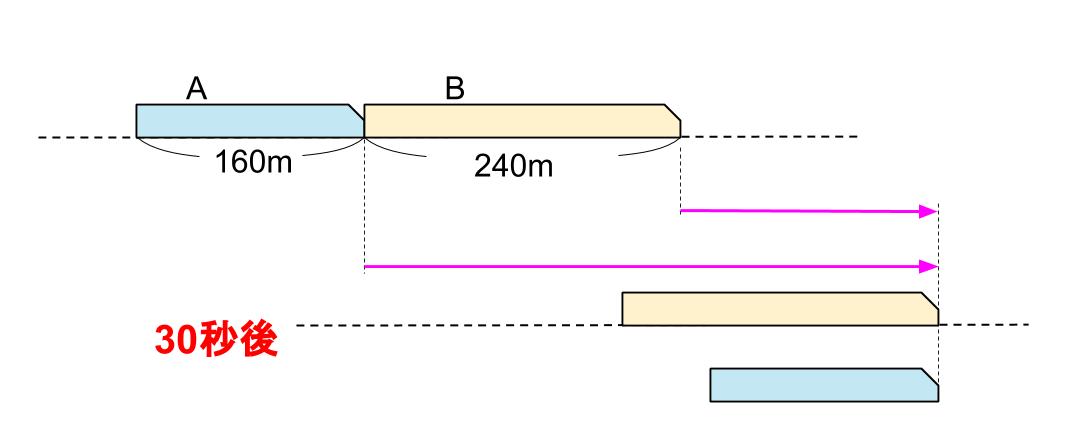

Aの先頭は、Bの先頭より、30秒で240m多く進んでいる。
240÷30=8
つまり、AはBよりも、秒速8mだけ速い。
Aの速さは秒速20mだから、
Bの速さは秒速12mです。

大正解!
素晴らしいね。
