異なる2種類の比の処理
和一定
例題
AとBの所持金の比ははじめ7:3でしたが、AがBに400円あげたので、2人の所持金の比は3:2になりました。はじめにAはいくら持っていましたか。
解説

この例題も2種類の比があります。
2種類の比の共通部分は・・・なさそうです。
「差が一定」も成り立たないですね。
今度こそ消去算ですかね。

うん、OK。
もちろん消去算で正しい答えがでるよ。
ただし今回も、別の視点を学習しましょう。
「差一定」がダメだったのだけれど、算数って「差」ともう1つあるよね・・・?

そうですね。
和に着目ですか?

うん、算数って「差」か「和」に着目することがほとんどでしょ。
あとは「何倍なのか」っていう比・割合に着目することもあるけどね。
大まかに着眼点はこの3つしかないんだ。

じゃあ、和に着目してみると・・・
あ、和が一定だ。
400円あげる前と後で、2人の所持金の和は変化しないです。
和を共通部分にすれば連比ができます!

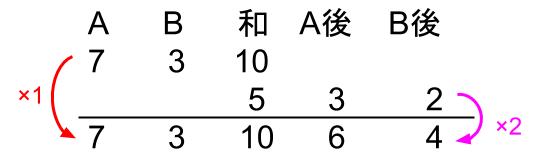
A⑦とB③
だったけど、
A⑥とB④
に変化した。
変化した理由は、AがBに400円あげたから。
つまり、①=400円だ。

素晴らしいね!このまま正解しちゃってください!

A⑦2800円とB③1200円
だったけど、
A⑥2400円とB④1600円
に変化した。
はじめのAは2800円です!

OK正解!!
「和一定」に気づけさえすれば、計算処理は差一定のときとほぼ同じだね!!

「差が一定」パターンと
「和が一定」パターンか。
なるほどねー。

異なる2つの比が共通部分でそろえられないとき、「差一定」か「和一定」に着目すると解けるときがあります。
このような基礎知識は、経験して覚えればいい。
今後似たような問題に対して、この解法を思い出すことができれば実力十分だよ。
「差一定」も「和一定」も、どちらも消去算(連立方程式)で解くことが可能です。
しかし、「差一定」と「和一定」はすぐに見抜けてほしいものです。

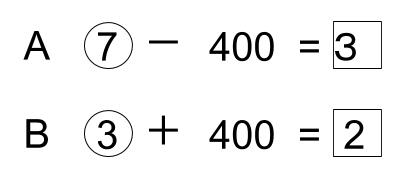
さて、この問題を消去算で解くとします。

普通の消去算ですね。
○をそろえても、□をそろえても解けます。
消去算をするだけで解決します。

そういうことです。
「和一定」に気づけなかったとしても、消去算をすることで解けるのです。
で、○をそろえても□をそろえても解けますが。
ところで、400はすでにそろっているね。

「-400」と「+400」の符号違いだから、和をとれば消えますね。

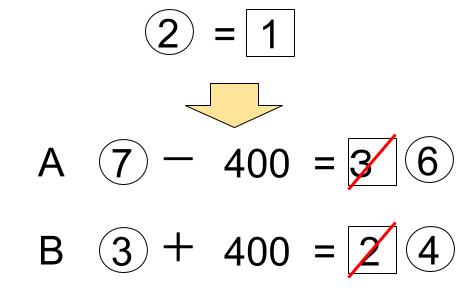
⑩=5だから、
②=1
これを使って、〇だけの式にすると

どちらの式からも、
①=400円がわかりますね。
これで解けました。

ちなみにこれは、一番はじめに「和一定」で解いたときと完全に同じ解き方をしているんだ。見た目は違うけどね。
きちんと「和一定」に気付いて、連比で解くことが最もおススメだよ。
消去算は連比より時間もかかるし、計算のための余白だってたくさん使うからね。