異なる2種類の比の処理
差一定
例題
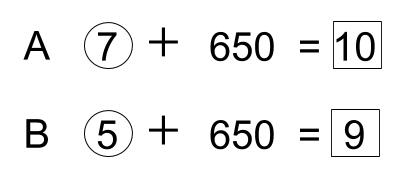
AとBの所持金の比は7:5でしたが、2人とも650円ずつもらったのでAとBの所持金の比は10:9になりました。はじめAはいくらもっていましたか。
解説

問題文中に2種類の比があるね。

はい。さすがにもう覚えました。
共通部分があればそろえる。
なければ消去算。
今回は・・・消去算かな。

○を35にそろえても解けるし、
□を90にそろえても解けます。
どちらで計算しようかな・・・

はい、その通りです。
残りの消去算はさすがにできますね。
あとは計算をやりきれば答えがでます。
それはそれで置いといて、今回は別の視点も学習しておきたい。
以前、こんな問題をやったんだけど、ちゃんとマスターしてるかな?
復習問題
現在、母は34才、子は6才です。母の年令が子の年令の3倍になるのは何年後ですか。

ああ、やったような気がします。
この問題のポイントは、「差が変化しない」でした。
母の年令が③
子の年令が①
になったとき、2人の差②=28
つまり、
母の年令が③=42
子の年令が①=14
これは、8年後ですね。

正解!ばっちり覚えているね!良かった。
今日の例題と、この復習問題って、ほとんど同じ問題でしょ。

ああ、確かに。
年齢の比が17:3だった母と子だけど、2人とも8歳年をとって、年齢の比が3:1になる。
2人とも650円もらったのが例題
2人とも8歳年をとるのが復習問題
2人とも同じだけ増えて、比が変化しています。
確かに似たような問題ですね。

その通り。
だからこの例題も、さっきの復習問題みたいに「差が変化しない」がポイントだよ。
650円もらう前と後で、差は等しいからね。
差が2つの比をつなぐんだ。

比をそろえた後で〇とか□とかをつけた数値にして処理すると良いです。
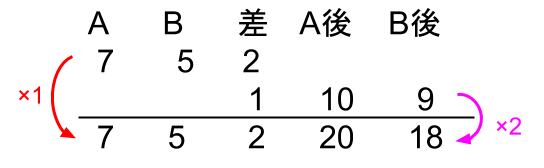
つまり、はじめのAは⑦、Bは⑤だったけど、2人とも650円もらって、
Aは⑳、Bは⑱になったのです。
AもBも⑬増えているでしょ。なぜって、2人とも650円もらったからね。
⑬=650円だよ。

なるほど。
650÷13=50
だから、
①=50ということか。
A:⑦350 → ⑳ 1000
B:⑤250 → ⑱ 900
うまく解けてます!
はじめのAは350円もっていました!

それで正解だよ。
自分のだした値で、文章題の条件全体とうまくいっているかを確かめることができるからね。必ずそこまでやること!
「差が一定」に気づくという、気づきの1ステップがあります。
しかし、そもそも「差が一定」を利用すればうまく解けるということを知らなければ、「差が一定」に着目できるはずもありません。
「差が一定」を利用すればうまくとけるタイプの問題がある、ということは知識・経験知なのです。
そして、どのようなときに差一定なのか、特徴的なのでこれも覚えてほしいのですが、どうしてもどうしても「差が一定」に気づけるようにならないならば、「消去算」で解いてしまえばもちろんOKなのです。

ところで・・・
差一定に気づかなければ「消去算」をすることになるわけだけど。

〇や□をそろえるまでもなく、650はすでにそろっているよね。
だから、650を消すことができるでしょ。

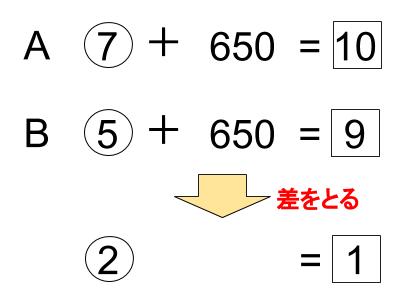
650の符号は+で同じ。
差をとればいいのか。

で?どうなるの?

続きがわからないなんて!
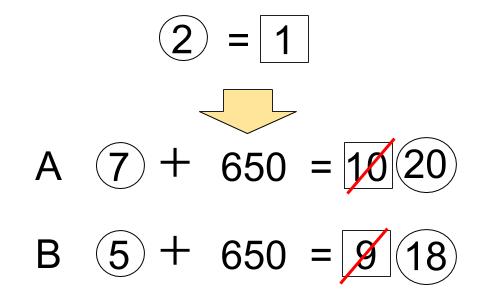
だって、②=1だよ。
2つの記号が結びついたんだ。だから、〇だけの式や□だけの式にできるということだよ。

なるほど。
⑬=650円が
2つの式、どちらからも得られますね。
これで解けますね。

ちなみにこれは、一番はじめに「差一定」で解いたときと完全に同じ解き方をしているんだ。見た目は違うけどね。
きちんと「差一定」に気付いて、連比で解くことが最もおススメなんだけどね。
消去算は連比より時間もかかるし、計算のための余白だってたくさん使うからね。
※4年生のときは、「差一定」は線分図でした。