異なる2種類の比の処理
割合の消去算
例題1
ある学校の昨年の生徒数は全部で520人でした。今年は男子が8%増え、女子が10%減ったので、全体では2人増えました。今年の女子は何人いますか。
解説

えっと・・・比がない?

何を愚かなことを・・・
「8%増える」や「10%減る」は損益でもやっていますよ!

そうでしたね。
男子は、昨年が100%で、今年が108%
女子は、昨年が100%で、今年が90%
ということですね。
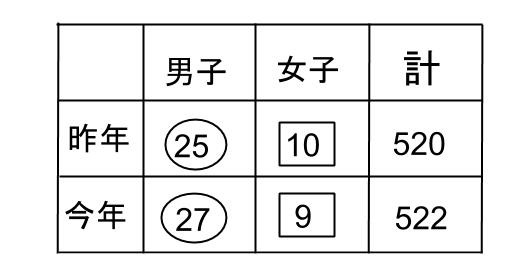
男子は、100:108=25:27
女子は、100:90=10:9
異なる2つの比の問題ですね。

はい、そいういうことです。
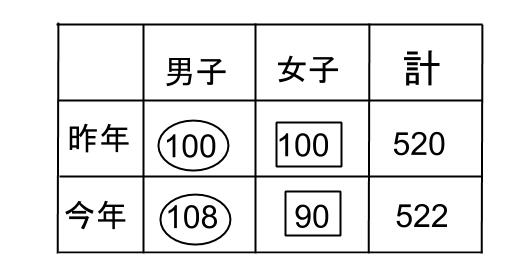
情報を表でまとめておきましょうか。
ところでこのタイプの問題は、比をもっとも簡単な比に直さない方が計算が楽なんだよ。
100%は100のままで解いていこうか。

へえ・・・なんでですか?

論理的に説明することじゃないな。
続きを見てくれればわかるよ。
経験としか言いようがないけどね。
さて、異なる2つの比の共通部分はあるかな?
なければ消去算だね。

これは消去算でしょう!
〇100+100=520
〇108+90=522
□を900にそろえて解けますね!

はい、あってます。
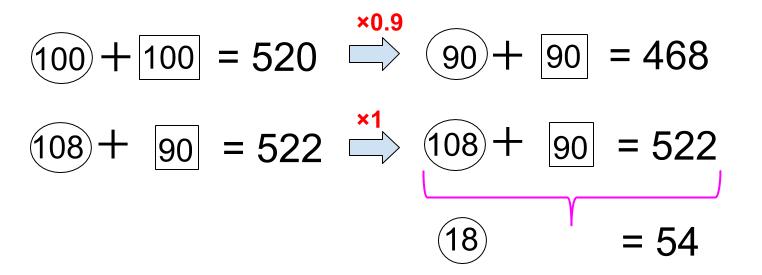
でも、ここは、□を90にそろえて解きましょうか。

⑱=54だから、①=3
今年の男子は、〇108=324
今年の女子は、522-324=198
求まりました。
198人です。

はい正解です。
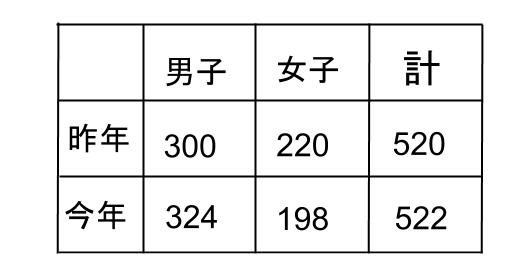
このタイプの問題は、他の数値もサッと求めて矛盾がないかの確認をしましょうね。

ところで、比を簡単にして解くとどうなるか。
ちょっと見ておこうかね。

今回は消去算がすこし面倒かも・・・

そういうことです。
さっきは0.9倍するだけでそろったよね。
とても楽な消去算だった。
でもね、今回は面倒な消去算かと言うと、実はそれほど大変ではないけどね。
小数が出てくるのを面倒がらずに、昨年を0.9倍してもよし。
〇22.5+9=468
あとは消去算をするだけだね。
あるいは、昨年の式は5で割れることに気づけると良いかな。
⑤+2=104
あとは、□を18にそろえて消すとかね。
あるいは、
男子は②増えて、女子は1減ったから、全体の差の2人は
②-1=2
とおけます。
これを利用して消去算するのも計算が楽ですね。
類題演習
ある商品AとBがあります。AもBも定価で買うと、代金の合計は1400円です。ある日、Aを定価の1割引き、Bを定価の2割引きで買ったところ、代金の合計は1195円でした。Aの定価はいくらですか。
解説

先の問題とまったく同じであることに気づいてくださいね。

Aの定価を⑩、Bの定価を10とすれば、
⑩+10=1400
⑨+8=1195
上の式を0.9倍すれば、
⑨+9=1260
実際の買い物の式との差をとる。
⑨+8=1195
1=65
つまり、Bの定価10は650円
Aの定価は、1400-650=750円
求まりました!

正解です!
A定価750円+B定価650円=1400円
A割引675円+B割引520円=1195円