比×比=比
過不足算を比で解く
導入例題
生徒全員にえんぴつを1人に5本ずつ、ボールペンを7本ずつ配った。配ったえんぴつの本数とボールペンの本数の比を求めなさい。
解説

なにこれ、めちゃくちゃ簡単じゃないですか。
5:7ですよ。
答えは5:7です。

うん。もちろん正解。
同じ人数に配っているからね。人数の比が1:1であると言える。
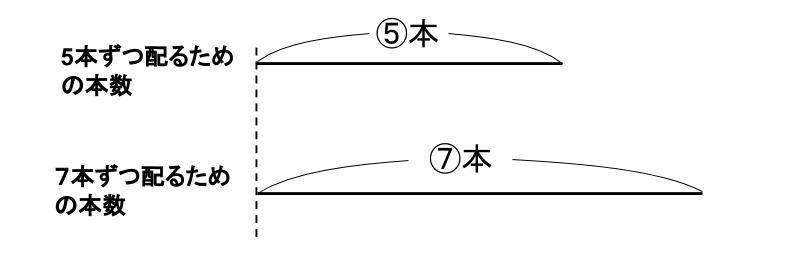
えんぴつ 5 × ①=⑤本
ボールペン 7 × ①=⑦本
こうやって出題されると簡単って思うよね。
でももちろんこんな問題は出題されない。
あたりまえで簡単なので、このようなことが問題として出題されることはないよ。
でもね、より複雑な文章題の中にひっそりとこの要素が隠れていることがあるんだ。そして、そのようなときは、これに気が付かない子の方が大多数だ。
代表例として「過不足算」を扱うよ。
例題1
生徒全員にえんぴつを1人に5本ずつ配ると14本余り、7本ずつ配るには4本足りない。このとき、えんぴつの本数を求めなさい。
解説

これはいわゆる「過不足算」です。
過不足算が苦手という子はものすごく多いのだけれど・・・
学くんは大丈夫かな?

どうだろう。やってみないとわからないな。
「過不足算」は久しぶりだから。

以前、「差を集める解法」を学習した。これはこれで身につけておいて欲しい。
しかし、この「差を集める解法」がどうしても苦手だという場合、これから説明する「比の解法」をマスターすればいい。
そして、「差を集める解法」が得意な子も、「比の解法」もマスターしてほしい。解法はいくつも持っていた方が強いからね。

ではいくよ。
線分図で整理する。
全員に5本ずつ配るときに必要な本数
全員に7本ずつ配るときに必要な本数
これを図示する。
ちなみに、⑤本と⑦本だよね。

なるほど、さっき確認した通りの5:7ですね。
⑤本と⑦本とおきますね。

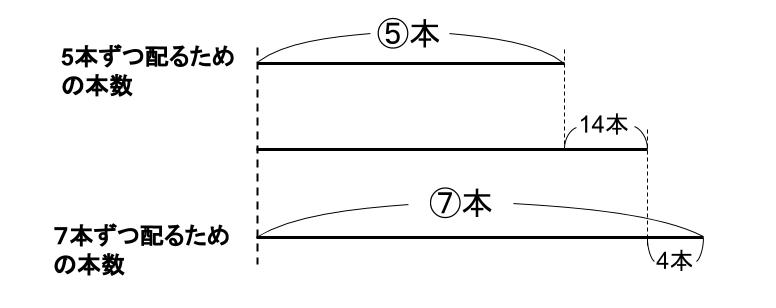
それでね、「実際の本数の線分図」を真ん中にかくのだ!やってごらん。

5本ずつ配ると14本余り、7本ずつ配るには4本足りない。

あ!!
②=14+4
がわかります!!

その通り!あとは計算するだけだね。
②=18なら、
①=9
じっさいの鉛筆は、⑤+14だから、45+14=59
答えは59本です。
ものすごく慣れてくれば、線分図なしで式処理だけで解いてもよい。
そのときは、以下のような等式から解くことになるよ。
じっさいの本数=⑤+14=⑦-4
よって、②=18
じっさいの本数=59本