比×比=比
これとは別の、もう1つの比の活用があります。
どちらも、受験算数における大きな柱であり、必ずマスターしなければいけません。
1:比×比=比
例題1
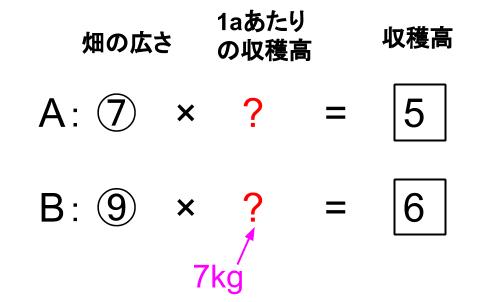
Aの畑の広さはBの畑の広さの\(\displaystyle \frac{7}{9}\) 倍で、Aの畑の豆の収穫高はBの畑の豆の収穫高の \(\displaystyle \frac{5}{6}\) 倍です。Bの畑の1aあたりの収穫高が7kgであるとすると、Aの畑の1aあたりの収穫高は何kgですか。
解説

何だか難しい言葉が並んでますね・・・よくわからないな・・・

1つ1つていねいに整理するしかないよね。
「収穫高」はわかる?
「Aの畑の豆の収穫高」というのは、Aの畑から取れる豆全体の量のことだ。
他に難しい言葉なんてないよね。「難しい言葉が並んでる」なんて言ってるけど、ほとんど問題文を読まないで逃げ出してるでしょ。
もう一度きちんと読んでごらん。話題は「収穫高」と他には何?

「収穫高」と・・・あとは
「畑の広さ」と「1aあたりの収穫高」ですね。
あ!
「畑の広さ」×「1aあたりの収穫高」=「収穫高」
ということですね。

その通り!
もう解けたも同然だ。あとは計算をきちんとやりきってくださいね。

Aの畑の広さはBの畑の広さの\(\displaystyle \frac{7}{9}\) 倍だから、
Aが⑦、Bが⑨とする。
Aの畑の豆の収穫高はBの畑の豆の収穫高の \(\displaystyle \frac{5}{6}\) 倍だから、
Aが5、Bが6とする。
Bの畑の1aあたりの収穫高は7kg
下のようになりますね。

B:〇63=6
ということだから、6で割れば、
〇10.5 =1
5をかけて、
〇52.5 =5
これを
A:⑦×?=5
の右に入れます。
つまり、
A:⑦×?=〇52.5
よって、?=\(\displaystyle \frac{52.5}{7}=7.5\)
求まりました!7.5㎏です。

正解ですね!
ところで、この問題は「食塩水」の構造とそっくりなんだ。
すぐにわからなくてもいいけどね。
食塩水では
「全体の量」×「濃さ(割合)」=「食塩の量」だ。
本問は、
「全体の面積」×「とれやすさ(割合)」=「収穫量」
つまり言いたいことは、「食塩水」においても同様の比の利用をする問題があるということです。食塩水を学習するときにくわしく見ていくことにしましょう。
別解1

ちょっと別の計算方法も見ておきましょう。
「比×比=比」という視点で見てみれば、「1aあたりの収穫高」の比を求めることができますよね。

A:7×\(\displaystyle \frac{5}{7}\)=5
B:9×\(\displaystyle \frac{6}{9}\)=6
なのだから、「1aあたりの収穫高」の比は、
\(\displaystyle \frac{5}{7}:\displaystyle \frac{6}{9}=15:14\)
「1aあたりの収穫高」は、Bの \(\displaystyle \frac{15}{14}\) 倍がA
7×\(\displaystyle \frac{15}{14}\) =7.5
求まりました!7.5㎏です。
別解2

ところで、「1aあたりの収穫高」の比を求めたければ、
同じ広さで比べればいいですよね。
A:⑦×?=5
B:⑨×?=6
だったのですから、どちらの畑のひろさも〇63にしてしまいましょう。
A:〇63×?=45
B:〇63×?=42
同じ広さからの収穫量が、45と42ですから、これこそが「1aあたりの収穫高」の比ですね。
45:42=15:14
このように求めることもできますね。