例題1・再掲
下の□にあてはまる数をそれぞれ答えなさい。
(1) 30は240の□倍です。
(2) □は60の \(\displaystyle \frac{4}{5}\) 倍です。
(3) 120は□の0.75倍です。
解説
分数の利用

引き続き、(3)の解説をしていくよ。
さきほど、
120=□×0.75
で、□の求め方が、120÷0.75だということが、迷わずにわかった子もいると思う。
この場合も、何も考えずに筆算をするのは絶対にダメ。
さっきも言ったど、割り切れる保証もないのだから。

じゃあどうするんですか?

さっき、\(30÷240=\displaystyle \frac{30}{240}\) ってやったでしょ。
\(a÷b=\displaystyle \frac{a}{b}\)
これが分数という表記の決め事です。
「わり算」と「分数」は同じもの、見た目が違うだけなんです。
だから、
\(120÷0.75=\displaystyle \frac{120}{0.75}\)
一切計算をせずに、ただ上下に並べる。
あとの処理は、さっきやった通りです。

なるほど。
とにかく「わり算」をしないのがコツなんですね。
等式の変形

他のやり方も見ておこう。
120=□×0.75
の□の求めかただ。
この式は、120と□×0.75が等しいという意味だ。
わかる?

はい。あたりまえですよ。

120=□×0.75のように、「=」で結ばれた式を「等式」と言うんだ。
左と右が等しいということを表している。
この式の、左も右も100倍してみよう。
左は、120×100
右は、□×0.75×100
どう、等しいかな?

等しいです。同じものがどちらも100倍になったのだから。

そうだよね。
120×100=□×0.75×100
と「等号」で結ばれる。
つまり、12000=□×75 だ。
では次に、左右どちらも75 で割ってみる。
どう?左と右は等しいままかな。

はい、等しいです。あたりまえですよ。

すると等式は、
\(\displaystyle \frac{12000}{75}=\displaystyle \frac{□×75}{75}\) となる。
つまり、
\(\displaystyle \frac{12000}{75}=□\)
だね。

なるほど。
あとは分数を簡単にすれば答えが求まるのか。
この方法も逆算って感じがしないですね。

そうだね。このやり方を使うと、
120=□×0.75
の□を求めるために
□=120÷0.75 なのか、□=120×0.75なのか迷うことがなくなるね。
上でみたような計算処理を、「等式の変形」と言うんだ。
「等式の変形」とは、等号(=)の左右に、まったく同じ計算をして変形することだよ。
塾でもほとんど教えられていないけど、算数の達人ならば確実に使っている重要な計算テクニックだよ。
正式に習うのは中学生になってからなんだけど、小学生にも十分理解できる内容だ。
とても有用なので、どんどん利用していかないといけないよ。
※ちなみに「消去算」ですでに「等式の変形」を使っていますね。

ところで、
120=□×0.75 を等式の変形で求めるとき、上のようにまず左右を100倍する必要はないよ。
はじめから、左右を0.75で割ってしまえばいい。
\(\displaystyle \frac{120}{0.75}=\displaystyle \frac{□×0.75}{0.75}\) となって、
つまり、
\(\displaystyle \frac{120}{0.75}=□\)
続きの計算は以前に説明した通りだよ。
分数に直せる小数の活用

結局、計算は分数の活用がとても重要だということがわかるよね。
どんどん分数を使っていくことが計算上手になるために必須なのだ。
分数は大事、という視点を持っている計算上手の人ならば、
120=□×0.75
は
0.75を分数になおします。

\(0.75=\displaystyle \frac{75}{100}\) ですね。

間違ってないけどね・・・
そこから毎回約分するのでは計算の素人丸出しです。
\(0.75=\displaystyle \frac{3}{4}\)
は絶対に暗記していないといけないのです。

そういえば・・・そんな話聞いたことあるかも・・・

つまり、
120=□×0.75
は
120=□×\(\displaystyle \frac{3}{4}\)
ということだ。
どう?□にはいる数の出し方は簡単かな?

分数はやっぱりちょっと苦手ですね・・・

たくさん計算練習をして慣れるしかないよ。
計算練習をすることで、分数の運用のルールを覚えていく。
運用できるようになってはじめて、分数がわかるようになるからね。
つまり、「わかる」から「できるようになる」のではなくて、
「できるようになりながら、わかっていく」のです。

??

まあ、先生を信じて、反復練習をすればいいってことです!
では、
120=□×\(\displaystyle \frac{3}{4}\)
の□の値の求めかたです。
この□に入る数の求め方はいろいろある。
どんなやり方で求めてもいいのだけれど、「等式の変形」がおすすめかな。
左右を4倍してみよう。

120×4=□×\(\displaystyle \frac{3}{4}\)×4
480=□×3
分母をはらうための4倍だったんですね。
続きはもうわかります。
□=480÷3=160
なるほど!

正解!さらなる計算のテクニックを伝えると
120×4=□×\(\displaystyle \frac{3}{4}\)×4
の次にかく等式は、
120×4=□×3
がよい。
今回は、120×4が暗算でできるほど簡単だから、大したロスにならないけれど、ここは計算する意味がないでしょ。
その後すぐに3で割るのだから。
120×4=□×3
左右を3で割ると
\(\displaystyle \frac{120×4}{3}=\displaystyle \frac{□×3}{3}\)
左右どちらも3で約分できますね。
40×4= □
160 = □

なるほどー

かけ算は保留しておく。そうすることで、手間が省けたり、その後の約分も簡単になることが多い。
これは一生使える計算テクニックだからね。
計算のテクニックを解説してきました。
どれもとても重要なことばかりです。
しっかり1つ1つ身につけていってください。
絶対にこうすればいいよ、という1つを提示することはできません。
日々、いろいろな計算方法を試していってください。そうやって数に対する感覚や、計算技術を高めていくしかありません。テスト(入試)本番で、日ごろから練習してこなかった方法をいきなり試すことはできませんので、常日頃からどれだけ試行錯誤を繰り返したかという愚直な積み重ねが、圧倒的な計算スピードの差としてあらわれることになります。
図によるまとめ

図でまとめておくよ。
AとB、2つの量があって、どちらかがどちらかの何倍になっているか。
これは以下のような図にまとめることができます。
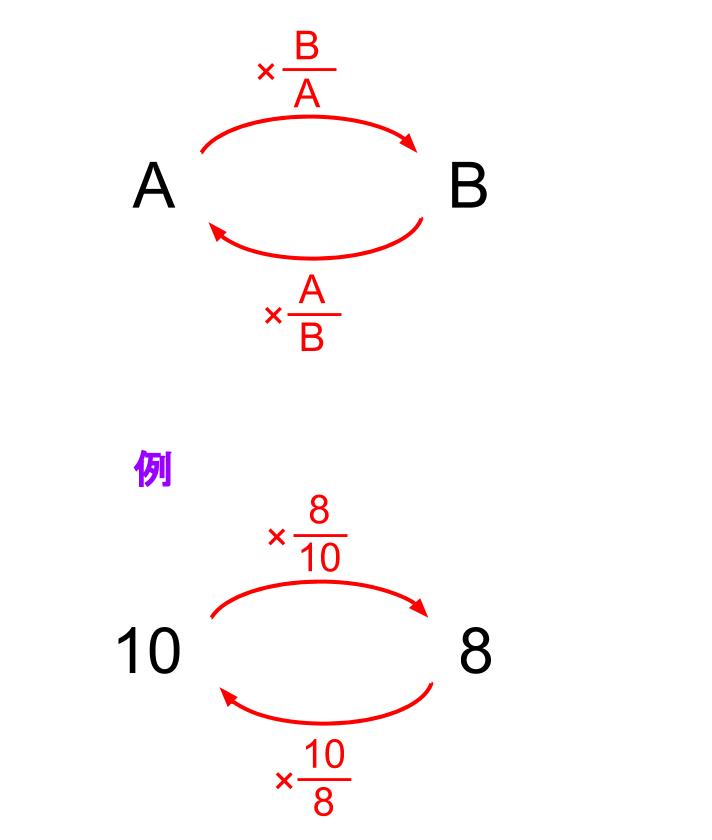

このように理解すれば、「逆算」も「わり算」もまったく必要がありません。
AとBを上下に並べて分数をつくるだけです。
必要あらば約分をしましょう。
ここで解説した計算ができるということが、算数における計算の基礎土台が固まったということです(数学と言っても良い)。
しかし、この計算の基礎土台が固まっていない状態で学習を続けている子が大半です。大手有名進学塾の中間層から上位層でさえ、この計算の基礎土台があやふやな子もたくさんいます。特に等式の変形はほとんどの子が使えません。大手進学塾でも、ていねいにこの計算テクニックを指導しないからです。
算数が得意になるための重要な分かれ道がここにあります。この計算を完璧に使えるようにすることが大事なのです。ピアノや水泳の反復練習と一緒です。何度も何度もくりかえして、体にしみこむまで練習しましょう。
