食塩水は「全体に対して部分がどれだけあるのか」という割合の代表選手です。非常に多くの学校で頻繁に出題される重要単元となります。
1:食塩水の導入
2:食塩水を図で整理する
例題3
食塩30gを水にとかして濃さが12%の食塩水を□gつくりました。
□にあてはまる値を求めなさい。
解説

こんな図ですね。
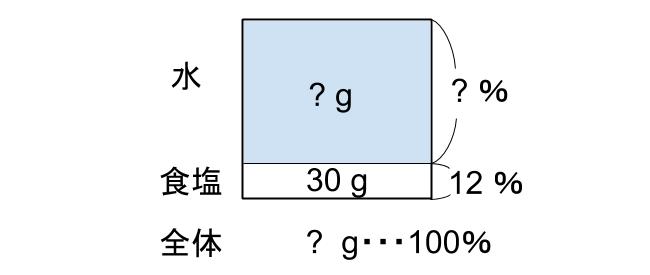

あ、わかりました。
30g=12%、
3で割れば、
10g=4%、
25倍すれば、
250g=100%
食塩水全体は250gです。

大正解!
公式にはめて解くならば、
\(\displaystyle \frac{30}{□}×100=12\)
あとは、□を計算で求めるだけ。
□=250

水はもちろん250-30=220g
全体の88%にあたります。
この問題でも使わない値だったけどね。

先生・・・ちょっと気になることが・・・
模式図の「水」のところなんですけど・・・
意味あるんですか?
全然使ってない気がするんですけど・・・

そうだね。使わないまま終わる問題ばかりを解いてきた。
でもね、使わないから意味がないなんてことはないよ。
初心者が食塩水をきちんと理解するためには、水もセットで考えていくべきなんだよ。
全体像がきちんと理解できて、はじめて真の理解に到達するからね。
それにね、「水」を使う問題だってあるんだよ。

はい、わかりました。
あともう1つ。
公式を完璧に覚えたら、図を省略して解いてもいいんですよね?

公式を暗記したくらいでは、図の省略をするのはまだはやいです。
省略はしちゃダメ。
公式一発では解けない問題もあるからね。
たくさんたくさん練習して、基礎がばっちり固まったならば図を省略しても良いんだけどね。
それは、模式図が完璧に頭に描けるレベルになったときだ。
「暗算」できる力がついたのならば、わざわざ紙上にかく必要はないからね。
